 |
Ш§ЩҶШ¬Щ…ЩҶ ШұШ§ ШҜШұ ЪҜЩҲЪҜЩ„ Щ…ШӯШЁЩҲШЁ Ъ©ЩҶЩҠШҜ :
|
|||||||
| Ш«ШЁШӘ ЩҶШ§Щ… | Ш§ШұШіШ§Щ„ ШҜШ№ЩҲШӘЩҶШ§Щ…ЩҮ ШЁЩҮ ШҜЩҲШіШӘШ§ЩҶ ! | ШұШ§ЩҮЩҶЩ…Ш§ЩҠ ШіШ§ЩҠШӘ | Community | ШӘЩӮЩҲЩҠЩ… | Ш§ШұШіШ§Щ„ЩҮШ§ЩҠ Ш§Щ…ШұЩҲШІ | Ш¬ШіШӘШ¬ЩҲ |
 |
| ШӘШЁЩ„ЩҠШәШ§ШӘ ШіШ§ЩҠШӘ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  |
|
|
LinkBack | Ш§ШЁШІШ§ШұЩҮШ§ЩҠ ШӘШ§ЩҫЩҠЪ© | ЩҶШӯЩҲЩҮ ЩҶЩ…Ш§ЩҠШҙ |
|
|
#1 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Щ…ЩӮШҜЩ…ЩҮвҖҢШ§ЩҠ ШЁШұ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ
Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШұШ§ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Щ…ЩҮЩ…ШӘШұЩҠЩҶ Щ…ШіШҰЩ„ЩҮ ШҜШұ ЩҠШ§ШҜЪҜЩҠШұЩҠ ШЁШҜЩҲЩҶ ЩҶШёШ§ШұШӘ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘ. Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ЩҠШ§ЩҒШӘЩҶ ЩҠЪ© ШіШ§Ш®ШӘШ§Шұ ШҜШұЩҲЩҶ ЩҠЪ© Щ…Ш¬Щ…ЩҲШ№ЩҮ Ш§ШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШҜЩҲЩҶ ШЁШұЪҶШіШЁ ШҜШұЪҜЩҠШұ Ш§ШіШӘ. Ш®ЩҲШҙЩҮвҖҢ ШЁЩҮ Щ…Ш¬Щ…ЩҲШ№ЩҮвҖҢШ§ЩҠ Ш§ШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ШЁЩҮ ЩҮЩ… ШҙШЁШ§ЩҮШӘ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЩҶШҜ. ШҜШұ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіШ№ЩҠ Щ…ЩҠвҖҢШҙЩҲШҜ ШӘШ§ ШҜШ§ШҜЩҮЩҮШ§ ШЁЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠЩҠ ШӘЩӮШіЩҠЩ… ШҙЩҲЩҶШҜ Ъ©ЩҮ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШҜШұЩҲЩҶ ЩҮШұ Ш®ЩҲШҙЩҮ ШӯШҜШ§Ъ©Ш«Шұ ЩҲ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШҜШұЩҲЩҶ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ Щ…ШӘЩҒШ§ЩҲШӘ ШӯШҜШ§ЩӮЩ„ ШҙЩҲШҜ.  ШҙЪ©Щ„ 1: ШҜШұ Ш§ЩҠЩҶ ШҙЪ©Щ„ ЩҶЩ…ЩҲЩҶЩҮвҖҢШ§ЩҠ Ш§ШІ Ш§Ш№Щ…Ш§Щ„ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШұЩҲЩҠ ЩҠЪ© Щ…Ш¬Щ…ЩҲШ№ЩҮ Ш§ШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ Щ…ШҙШ®Шө ШҙШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ Ш§ШІ Щ…Ш№ЩҠШ§Шұ ЩҒШ§ШөЩ„ЩҮ(Distance) ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Ш№ШҜЩ… ШҙШЁШ§ЩҮШӘ(Dissimilarity) ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШҜШұ Щ…ЩӮШ§ШЁЩ„ Ш·ШЁЩӮЩҮвҖҢвҖҢШЁЩҶШҜЩҠ ШҜШұ Ш·ШЁЩӮЩҮвҖҢШЁЩҶШҜЩҠ ЩҮШұ ШҜШ§ШҜЩҮ ШЁЩҮ ЩҠЪ© Ш·ШЁЩӮЩҮ (Ъ©Щ„Ш§Ші) Ш§ШІ ЩҫЩҠШҙЩҠЩҶ Щ…ШҙШ®Шө ШҙШҜЩҮ ШӘШ®ШөЩҠШө Щ…ЩҠвҖҢЩҠШ§ШЁШҜ ЩҲЩ„ЩҠ ШҜШұ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҮЩҠЪҶ Ш§Ш·Щ„Ш§Ш№ЩҠ Ш§ШІ Ъ©Щ„Ш§ШіЩҮШ§ЩҠ Щ…ЩҲШ¬ЩҲШҜ ШҜШұЩҲЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ЩҲШ¬ЩҲШҜ ЩҶШҜШ§ШұШҜ ЩҲ ШЁЩҮ Ш№ШЁШ§ШұШӘЩҠ Ш®ЩҲШҜ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ЩҶЩҠШІ Ш§ШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ Ш§ШіШӘШ®ШұШ§Ш¬ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ШҜШұ ШҙЪ©Щ„ ШІЩҠШұ ШӘЩҒШ§ЩҲШӘ ШЁЩҠЩҶ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҲ Ш·ШЁЩӮЩҮвҖҢШЁЩҶШҜЩҠ ШЁЩҮШӘШұ ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  a  b ШҙЪ©Щ„ 2: a) ШҜШұ Ш·ШЁЩӮЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ ЩҠЪ© ШіШұЩҠ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ Ш§ЩҲЩ„ЩҠЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁЩҮ ШҜШіШӘЩҮвҖҢЩҮШ§ЩҠ Щ…Ш№Щ„ЩҲЩ…ЩҠ ЩҶШіШЁШӘ ШҜШ§ШҜЩҮвҖҢ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ШҜШұ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§Щ„ЪҜЩҲШұЩҠШӘЩ… Ш§ЩҶШӘШ®Ш§ШЁ ШҙШҜЩҮ ШЁЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠЩҠ ЩҶШіШЁШӘ ШҜШ§ШҜЩҮвҖҢ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | 3ngineer (Ы°Ыҙ-ЫұЫҙ-ЫұЫіЫ№Ыҙ), dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), engineer_yasin (Ы°Ыҙ-ЫІЫ№-ЫұЫіЫёЫ№), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), farshad1362 (Ы°Ы№-ЫұЫ°-ЫұЫіЫ№Ы°), hamedmehdihamed (ЫұЫІ-ЫІЫ¶-ЫұЫіЫ№Ы°), hamidrezas (Ы°ЫІ-ЫІЫҙ-ЫұЫіЫ№Ы°), ITman2010 (Ы°Ыі-ЫұЫ№-ЫұЫіЫ№Ыұ), mozhdeh65 (Ы°Ыё-ЫұЫ№-ЫұЫіЫ№Ы°), redeemer (ЫұЫ°-ЫІ-ЫұЫіЫ№ЫІ), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°), samane_89 (Ы°ЫІ-ЫІЫө-ЫұЫіЫ№Ы°) |
| #ADS | |
|
ЩҶШҙШ§ЩҶ ШҜЩҮЩҶШҜЩҮ ШӘШЁЩ„ЫҢШәШ§ШӘ
ШӘШЁЩ„ЩҠШәЪҜШұ
ШӘШ§ШұЩҠШ® Ш№Ш¶ЩҲЩҠШӘ: -
Щ…ШӯЩ„ ШіЩғЩҲЩҶШӘ: -
ШіЩҶ: 2010
ЩҫШіШӘ ЩҮШ§: -
|
|
|
|
|
|
#2 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
ЩҠШ§ШҜЪҜЩҠШұЩҠ ШЁШ§ ЩҶШёШ§ШұШӘ ШҜШұ Щ…ЩӮШ§ШЁЩ„ ЩҠШ§ШҜЪҜЩҠШұЩҠ ШЁШҜЩҲЩҶвҖҢЩҶШёШ§ШұШӘ
ШҜШұ ЩҠШ§ШҜЪҜЩҠШұЩҠ ШЁШ§ ЩҶШёШ§ШұШӘ Ш§ШІ Ш§ШЁШӘШҜШ§ ШҜШіШӘЩҮвҖҢЩҮШ§ Щ…ШҙШ®Шө ЩҮШіШӘЩҶШҜ ЩҲ ЩҮШұ ЩҠЪ© Ш§ШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШўЩ…ЩҲШІШҙЩҠ ШЁЩҮ ШҜШіШӘЩҮвҖҢШ§ЩҠ Ш®Ш§Шө ЩҶШіШЁШӘ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ ЩҲ Ш§ШөШ·Щ„Ш§ШӯШЈ ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ ЩҶШ§ШёШұЩҠ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ Ъ©ЩҮ ШҜШұ ЩҮЩҶЪҜШ§Щ… ШўЩ…ЩҲШІШҙ Ш§Ш·Щ„Ш§Ш№Ш§ШӘЩҠ Ш№Щ„Ш§ЩҲЩҮ ШЁШұ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШўЩ…ЩҲШІШҙ ШҜШұ Ш§Ш®ШӘЩҠШ§Шұ ЩҠШ§ШҜЪҜЩҠШұЩҶШҜЩҮ (Learner) ЩӮШұШ§Шұ Щ…ЩҠвҖҢШҜЩҮШҜ. ЩҲЩ„ЩҠ ШҜШұ ЩҠШ§ШҜЪҜЩҠШұЩҠ ШЁШҜЩҲЩҶ ЩҶШёШ§ШұШӘ ЩҮЩҠЪҶ Ш§Ш·Щ„Ш§Ш№Ш§ШӘЩҠ ШЁШ¬ШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШўЩ…ЩҲШІШҙЩҠ ШҜШұ Ш§Ш®ШӘЩҠШ§Шұ ЩҠШ§ШҜЪҜЩҠШұЩҶШҜЩҮ ЩӮШұШ§Шұ ЩҶШҜШ§ШұШҜ ЩҲ Ш§ЩҠЩҶ ЩҠШ§ШҜЪҜЩҠШұЩҶШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ ШЁШ§ЩҠШіШӘЩҠ ШҜШұ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁЩҮ ШҜЩҶШЁШ§Щ„ ШіШ§Ш®ШӘШ§ШұЩҠ Ш®Ш§Шө ШЁЪҜШұШҜШҜ. |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), farshad1362 (Ы°Ы№-ЫұЫ°-ЫұЫіЫ№Ы°), hamidrezas (Ы°ЫІ-ЫІЫҙ-ЫұЫіЫ№Ы°), mozhdeh65 (Ы°Ыё-ЫұЫ№-ЫұЫіЫ№Ы°), redeemer (ЫұЫ°-ЫІ-ЫұЫіЫ№ЫІ), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°) |
|
|
#3 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Ъ©Ш§ШұШЁШұШҜЩҮШ§
Ш§ШІ ШўЩҶШ¬Ш§ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҠЪ© ШұЩҲШҙ ЩҠШ§ШҜЪҜЩҠШұЩҠ ШЁШҜЩҲЩҶ ЩҶШёШ§ШұШӘ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢЪҜШұШҜШҜШҢ ШҜШұ Щ…ЩҲШ§ШұШҜ ШЁШіЩҠШ§ШұЩҠ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶШҜ Ъ©Ш§ШұШЁШұШҜ ШҜШ§ШҙШӘЩҮвҖҢ ШЁШ§ШҙШҜ * ШҜШұ ШЁШ§ШІШ§ШұЩҠШ§ШЁЩҠ (Marketing): ШҜШіШӘЩҮвҖҢвҖҢШЁЩҶШҜЩҠ Щ…ШҙШӘШұЩҠвҖҢЩҮШ§ ШЁЩҮ ШҜШіШӘЩҮвҖҢЩҮШ§ЩҠЩҠ ШЁШұ ШӯШіШЁ ШұЩҒШӘШ§ШұЩҮШ§ ЩҲ ЩҶЩҠШ§ШІЩҮШ§ЩҠ ШўЩҶЩҮШ§ Ш§ШІ Ш·ШұЩҠЩӮ Щ…Ш¬Щ…ЩҲШ№ЩҮ ШІЩҠШ§ШҜЩҠ Ш§ШІ ЩҲЩҠЪҳЪҜЩҠвҖҢЩҮШ§ ЩҲ ШўШ®ШұЩҠЩҶ Ш®ШұЩҠШҜвҖҢЩҮШ§ЩҠ ШўЩҶЩҮШ§. * ШІЩҠШіШӘвҖҢвҖҢвҖҢШҙЩҶШ§ШіЩҠ (Biology): ШҜШіШӘЩҮвҖҢШЁЩҶШҜЩҠ ШӯЩҠЩҲШ§ЩҶШ§ШӘ ЩҲ ЪҜЩҠШ§ЩҮШ§ЩҶ Ш§ШІ ШұЩҲЩҠ ЩҲЩҠЪҳЪҜЩҠвҖҢЩҮШ§ЩҠ ШўЩҶЩҮШ§ * Ъ©ШӘШ§ШЁШҜШ§ШұЩҠ : ШҜШіШӘЩҮвҖҢШЁЩҶШҜЩҠ Ъ©ШӘШ§ШЁЩҮШ§ * ЩҶЩӮШҙЩҮвҖҢШЁШұШҜШ§ШұЩҠ ШҙЩҮШұЩҠ (City-Planning): ШҜШіШӘЩҮвҖҢШЁЩҶШҜЩҠ Ш®Ш§ЩҶЩҮвҖҢЩҮШ§ ШЁШұ Ш§ШіШ§Ші ЩҶЩҲШ№ ЩҲ Щ…ЩҲЩӮШ№ЩҠШӘ Ш¬ШәШұШ§ЩҒЩҠШ§ЩҠЩҠ ШўЩҶЩҮШ§. * Щ…Ш·Ш§Щ„Ш№Ш§ШӘ ШІЩ„ШІЩ„ЩҮвҖҢЩҶЪҜШ§ШұЩҠ (Earthquake studies): ШӘШҙШ®ЩҠШө Щ…ЩҶШ§Ш·ЩӮ ШӯШ§ШҜШ«ЩҮвҖҢШ®ЩҠШІ ШЁШұ Ш§ШіШ§Ші Щ…ШҙШ§ЩҮШҜШ§ШӘ ЩӮШЁЩ„ЩҠ. * ЩҲШЁ (WWW): ШҜШіШӘЩҮвҖҢШЁЩҶШҜЩҠ Ш§ШіЩҶШ§ШҜ ЩҲ ЩҠШ§ ШҜШіШӘЩҮвҖҢШЁЩҶШҜЩҠ Щ…ШҙШӘШұЩҠШ§ЩҶ ШЁЩҮ ШіШ§ЩҠШӘЩҮШ§ ЩҲ .... * ШҜШ§ШҜЩҮ Ъ©Ш§ЩҲЩҠ (Data Mining): Ъ©ШҙЩҒ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ ЩҲ ШіШ§Ш®ШӘШ§Шұ Ш¬ШҜЩҠШҜ Ш§ШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ Щ…ЩҲШ¬ЩҲШҜ * ШҜШұ ШӘШҙШ®ЩҠШө ЪҜЩҒШӘШ§Шұ (Speech Recognition): ШҜШұ ШіШ§Ш®ШӘ Ъ©ШӘШ§ШЁ Ъ©ШҜ Ш§ШІ ШЁШұШҜШ§ШұЩҮШ§ЩҠ ЩҲЩҠЪҳЪҜЩҠШҢ ШҜШұ ШӘЩӮШіЩҠЩ… Ъ©ШұШҜЩҶ ЪҜЩҒШӘШ§Шұ ШЁШұ ШӯШіШЁ ЪҜЩҲЩҠЩҶШҜЪҜШ§ЩҶ ШўЩҶ ЩҲ ЩҠШ§ ЩҒШҙШұШҜЩҮвҖҢШіШ§ШІЩҠ ЪҜЩҒШӘШ§Шұ * ШҜШұ ШӘЩӮШіЩҠЩ…вҖҢШЁЩҶШҜЩҠ ШӘШөШ§ЩҲЩҠШұ(Image Segmentation): ШӘЩӮШіЩҠЩ…вҖҢШЁЩҶШҜЩҠ ШӘШөШ§ЩҲЩҠШұ ЩҫШІШҙЪ©ЩҠ ЩҲ ЩҠШ§ Щ…Ш§ЩҮЩҲШ§ШұЩҮвҖҢШ§ЩҠ |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | 3ngineer (Ы°Ыҙ-ЫұЫҙ-ЫұЫіЫ№Ыҙ), dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), farshad1362 (Ы°Ы№-ЫұЫ°-ЫұЫіЫ№Ы°), hamidrezas (Ы°ЫІ-ЫІЫҙ-ЫұЫіЫ№Ы°), redeemer (ЫұЫ°-ЫІ-ЫұЫіЫ№ЫІ), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°) |
|
|
#4 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Щ…ШіШ§ШҰЩ„ ШҜШұЪҜЩҠШұ ШЁШ§ ШұЩҲШҙвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Щ…ЩҲШ¬ЩҲШҜ
Щ…ШӘШЈШіЩҒШ§ЩҶЩҮ ЪҶЩҶШҜЩҠЩҶ Щ…ШіШҰШ§Щ„ЩҮ ШҜШұ Ш®ШөЩҲШө ШұЩҲШҙвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Щ…Ш·ШұШӯ Ш§ШіШӘ Ъ©ЩҮ ЩҮЩҶЩҲШІ ШЁЩҮ ШҙЪ©Щ„ Ъ©Ш§Щ…Щ„ ЩҫШ§ШіШ® ШҜШ§ШҜЩҮ ЩҶШҙШҜЩҮвҖҢШ§ЩҶШҜ. ЩҲ ЩҮЩ…ЪҶЩҶШ§ЩҶ ШӘЩ„Ш§ШҙвҖҢЩҮШ§ЩҠ ШЁШіЩҠШ§ШұЩҠ ШЁЩҮ Щ…ЩҶШёЩҲШұ ШӯЩ„ ШўЩҶЩҮШ§ Ш§ЩҶШ¬Ш§Щ… Щ…ЩҠвҖҢЪҜЩҠШұШҜ. В· ШұЩҲШҙвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩӮШ§ШҜШұ ЩҶЩҠШіШӘЩҶШҜ ШӘЩ…Ш§Щ…ЩҠ ЩҶЩҠШ§ШІЩҮШ§ЩҠ Щ…ШіШ§ШҰЩ„ ШұШ§ ШЁЩҮ Ш·ЩҲШұ ЩҮЩ…вҖҢШІЩ…Ш§ЩҶ ШЁШұШўЩҲШұШҜЩҮвҖҢЪ©ЩҶЩҶШҜ. В· ШЁЩҮ ШҜЩ„ЩҠЩ„ ЩҫЩҠЪҶЩҠШҜЪҜЩҠвҖҢ Щ…ШӯШ§ШіШЁШ§ШӘЩҠ ШІЩҠШ§ШҜ ШҜШұ ШЁШұШ®ЩҲШұШҜ ШЁШ§ Щ…Ш¬Щ…ЩҲШ№ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШІШұЪҜ ШЁШ§ ШӘШ№ШҜШ§ШҜ ШҜШ§ШҜЩҮ вҖҢШІЩҠШ§ШҜ ЩҲ ШӘШ№ШҜШ§ШҜ ЩҲЩҠЪҳЪҜЩҠвҖҢЩҮШ§ЩҠ ШІЩҠШ§ШҜ ШЁШұШ§ЩҠ ЩҮШұ ШҜШ§ШҜЩҮ Ш№Щ…Щ„ЩҠ ЩҶЩҠШіШӘЩҶШҜ. В· ШЁЩҮ ШҜЩ„ЩҠЩ„ ЩҲШ§ШЁШіШӘЪҜЩҠвҖҢ ШҙШҜЩҠШҜ ШЁЩҮ ШӘШ№ШұЩҠЩҒ Щ…Ш№ЩҠШ§Шұ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШҜШұ Щ…ШіШ§ШҰЩ„ЩҠ Ъ©ЩҮ ШӘШ№ШұЩҠЩҒ Щ…Ш№ЩҠШ§Шұ ШҙШЁШ§ЩҮШӘ Щ…ШҙЪ©Щ„ ШЁШ§ШҙШҜ ЩҶШӘШ§ЩҠШ¬ Щ…Ш·Щ„ЩҲШЁЩҠ ШӘЩҲЩ„ЩҠШҜ ЩҶЩ…ЩҠвҖҢЪ©ЩҶЩҶШҜ.(ШҜШұ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҲЩҠЪҳЪҜЩҠвҖҢ ШІЩҠШ§ШҜ) В· ШЁШұШ§ЩҠ ЩҶШӘШ§ЩҠШ¬ ШўЩҶЩҮШ§ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ ШӘЩҒШіЩҠШұЩҮШ§ЩҠ Щ…Ш®ШӘЩ„ЩҒЩҠ ШЁЩҠШ§ЩҶ Ъ©ШұШҜ. Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШҜШұ Щ…ЩӮШ§ШЁЩ„ ЪҶЩҶШҜЩҠвҖҢШіШ§ШІЩҠ ШЁШұШҜШ§ШұЩҠ ЩҮЩ…Ш§ЩҶвҖҢЪҜЩҲЩҶЩҮ Ъ©ЩҮ ШЁШӯШ« ШҙШҜШҢ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҶЩҲШ№ЩҠ ШіШ§ШІЩ…Ш§ЩҶШҜЩҮЩҠ ШҜШ§ШҜЩҮвҖҢЩҮШ§ Ш§ШіШӘШҢ ШЁШұ Ш§ШіШ§Ші ШҙШЁШ§ЩҮШӘЩҠ Ъ©ЩҮ ШЁЩҠЩҶ ШўЩҶЩҮШ§ ШӘШ№ШұЩҠЩҒ Щ…ЩҠвҖҢШҙЩҲШҜ ШЁЩҮ ЪҜЩҲЩҶЩҮвҖҢШ§ЩҠ Ъ©ЩҮ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠЩҠ Ъ©ЩҮ ШҜШұЩҲЩҶ ЩҠЪ© Ш®ЩҲШҙЩҮ ЩӮШұШ§Шұ Щ…ЩҠвҖҢЪҜЩҠШұЩҶШҜШҢ ЩҶШіШЁШӘ ШЁЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠЩҠ Ъ©ЩҮ ШҜШұЩҲЩҶ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ Щ…ШӘЩҒШ§ЩҲШӘ ЩӮШұШ§Шұ Щ…ЩҠвҖҢЪҜЩҠШұЩҶШҜШҢ ШЁЩҠШҙШӘШұ ШЁШ§ШҙШҜ. ШҜШұ Ъ©Ш§ШұШЁШұШҜЩҮШ§ЩҠ Ш§ШұШӘШЁШ§Ш·ЩҠ ЩҲ ЩҒШҙШұШҜЩҮвҖҢШіШ§ШІЩҠ ШҜШ§ШҜЩҮвҖҢЩҮШ§ Ш§ШІ ШұЩҲШҙЩҮШ§ЩҠЩҠ ШЁЩҮ ЩҶШ§Щ… ЪҶЩҶШҜЩҠвҖҢШіШ§ШІЩҠ ШЁШұШҜШ§ШұЩҠ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ Ш§ШІ ШЁШ№Ш¶ЩҠ Ш¬ЩҶШЁЩҮвҖҢЩҮШ§ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ ШўЩҶЩҮШ§ ШұШ§ Щ…Ш№Ш§ШҜЩ„ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘ. ШҜШұ ЪҶЩҶШҜЩҠвҖҢШіШ§ШІЩҠ ШЁШұШҜШ§ШұЩҠ ЩҶЩҠШІ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁШұ Ш§ШіШ§Ші Щ…ЩҠШІШ§ЩҶ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШўЩҶЩҮШ§ ШЁЩҮ ШҜШіШӘЩҮвҖҢЩҮШ§ЩҠЩҠ ШӘЩӮШіЩҠЩ… Щ…ЩҠ ШҙЩҲЩҶШҜ ЩҲ ЩҮШұ ШҜШіШӘЩҮ ШЁЩҲШіЩҠЩ„ЩҮ ЩҠЪ© ШЁШұШҜШ§Шұ Ъ©ЩҮ ШЁЩҮ ШўЩҶ Ъ©Щ„Щ…ЩҮ Ъ©ШҜ (CodeWord) ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ Ш¬Ш§ЩҠЪҜШІЩҠЩҶ Щ…ЩҠвҖҢЪҜШұШҜШҜ. ШЁЩҮ Щ…Ш¬Щ…ЩҲШ№Ш© Ш§ЩҠЩҶ Ъ©Щ„Щ…Ш§ШӘЩҗ Ъ©ШҜ Ш§ШөШ·Щ„Ш§ШӯШЈ Ъ©ШӘШ§ШЁЩҗ Ъ©ШҜ(CodeBook) ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШҜШұШЁШ№Ш¶ЩҠ Ш§ШІ ШЁШ®Ш«вҖҢЩҮШ§ЩҠ Ш№Щ„Щ…ЩҠ ШЁЩҠЩҶ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҲ ЪҶЩҶШҜЩҠвҖҢШіШ§ШІЩҠ ШЁШұШҜШ§ШұЩҠ ШӘЩҒШ§ЩҲШӘЩҮШ§ЩҠЩҠ ЩӮШ§ШҰЩ„ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ШІЩҠШұШ§ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШұШ§ ЩҠЪ© ШұЩҮЩҠШ§ЩҒШӘ ШЁШҜЩҲЩҶ ЩҶШёШ§ШұШӘ ШЁШұШ§ЩҠ ШӘШӯЩ„ЩҠЩ„ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШҜШұ ЩҶШёШұ Щ…ЩҠвҖҢЪҜЩҠШұЩҶШҜ ЩҲЩ„ЩҠ ЪҶЩҶШҜЩҠвҖҢШіШ§ШІЩҠ ШЁШұШҜШ§ШұЩҠ ШұШ§ ШұЩҲШҙЩҠ ШЁШұШ§ЩҠ Ъ©ШҙЩҒ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ЩҶЩ…ЩҠвҖҢШҙЩҶШ§ШіЩҶШҜ ШЁЩ„Ъ©ЩҮ ШўЩҶ ШұШ§ ШұШ§ЩҮЩҠ ШЁШұШ§ЩҠ ЩҶЩ…Ш§ЩҠШҙ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁШ§ ШӘШ№ШҜШ§ШҜ Ш№ЩҶШ§ШөШұ Ъ©Щ…ШӘШұ ШЁЩҮ ЪҜЩҲЩҶЩҮвҖҢШ§ЩҠ Ъ©ЩҮ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ Ш§ШІ ШҜШіШӘ ШұЩҒШӘЩҮ ШӯШҜШ§ЩӮЩ„ ШҙЩҲШҜШҢ Щ…ЩҠвҖҢШҙЩҶШ§ШіЩҶШҜ. Ш№Щ„ЩҠвҖҢШұШәЩ… ШӘЩҒШ§ЩҲШӘ ШЁЩҠШ§ЩҶ ШҙШҜЩҮ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ ШұЩҲШҙЩҮШ§ЩҠ ШЁЪ©Ш§Шұ ШұЩҒШӘЩҮ ШҜШұ ЩҮШұ ЩҠЪ© ШўЩҶЩҮШ§ ШұШ§ ШҜШұ ШҜЩҠЪҜШұ ЩҶЩҠШІ ШЁЪ©Ш§Шұ ШЁШұШҜ ШҜШұ Ш§ЩҠЩҶШ¬Ш§ ШЁЩҠЩҶ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҲ ЪҶЩҶШҜЩҠвҖҢШіШ§ШІЩҠ ШЁШұШҜШ§ШұЩҠ ШӘЩҒШ§ЩҲШӘЩҠ ЩӮШ§ШҰЩ„ ЩҶЩ…ЩҠвҖҢШҙЩҲЩҠЩ…. |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), hamidrezas (Ы°ЫІ-ЫІЫҙ-ЫұЫіЫ№Ы°), redeemer (ЫұЫ°-ЫІ-ЫұЫіЫ№ЫІ), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°) |
|
|
#5 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
ШұЩҲШҙвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ
ШұЩҲШҙвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШұШ§ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ Ш§ШІ ЪҶЩҶШҜЩҠЩҶ Ш¬ЩҶШЁЩҮ ШӘЩӮШіЩҠЩ…вҖҢШЁЩҶШҜЩҠ Ъ©ШұШҜ: 1- Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Ш§ЩҶШӯШөШ§ШұЩҠ (Exclusive or Hard Clustering) ЩҲ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ЩҮЩ…вҖҢЩҫЩҲШҙЩҠ (Overlapping or Soft Clustering) ШҜШұ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Ш§ЩҶШӯШөШ§ШұЩҠ ЩҫШі Ш§ШІ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҮШұ ШҜШ§ШҜЩҮ ШҜЩӮЩҠЩӮШЈ ШЁЩҮ ЩҠЪ© Ш®ЩҲШҙЩҮ ШӘШ№Щ„ЩӮ Щ…ЩҠвҖҢЪҜЩҠШұШҜ Щ…Ш§ЩҶЩҶШҜ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ K-Means. ЩҲЩ„ЩҠ ШҜШұ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ЩҮЩ…ЩҫЩҲШҙЩҠ ЩҫШі Ш§ШІ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁЩҮ ЩҮШұ ШҜШ§ШҜЩҮ ЩҠЪ© ШҜШұШ¬ЩҮ ШӘШ№Щ„ЩӮ ШЁШ§ШІШ§ШЎ ЩҮШұ Ш®ЩҲШҙЩҮ ЩҶШіШЁШӘ ШҜШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШЁЩҮ Ш№ШЁШ§ШұШӘЩҠ ЩҠЪ© ШҜШ§ШҜЩҮ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶШҜ ШЁШ§ ЩҶШіШЁШӘЩҮШ§ЩҠ Щ…ШӘЩҒШ§ЩҲШӘЩҠ ШЁЩҮ ЪҶЩҶШҜЩҠЩҶ Ш®ЩҲШҙЩҮ ШӘШ№Щ„ЩӮ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ. ЩҶЩ…ЩҲЩҶЩҮвҖҢШ§ЩҠ Ш§ШІ ШўЩҶ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҒШ§ШІЩҠ Ш§ШіШӘ. 2- Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ (Hierarchical) ЩҲ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Щ…ШіШ·Шӯ(Flat) ШҜШұ ШұЩҲШҙ Ш®ЩҲШҙЩҮ ШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠШҢ ШЁЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ ЩҶЩҮШ§ЩҠЩҠ ШЁШұ Ш§ШіШ§Ші Щ…ЩҠШІШ§ЩҶ Ш№Щ…ЩҲЩ…ЩҠШӘ ШўЩҶЩҮШ§ ШіШ§Ш®ШӘШ§ШұЩҠ ШіЩ„ШіЩ„ЩҮвҖҢ Щ…ШұШ§ШӘШЁЩҠ ЩҶШіШЁШӘ ШҜШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. Щ…Ш§ЩҶЩҶШҜ ШұЩҲШҙ Single Link. ЩҲЩ„ЩҠ ШҜШұ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Щ…ШіШ·Шӯ ШӘЩ…Ш§Щ…ЩҠ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ ЩҶЩҮШ§ЩҠЩҠ ШҜШ§ШұШ§ЩҠ ЩҠЪ© Щ…ЩҠШІШ§ЩҶ Ш№Щ…ЩҲЩ…ЩҠШӘ ЩҮШіШӘЩҶШҜ Щ…Ш§ЩҶЩҶШҜ K-Means. ШЁЩҮ ШіШ§Ш®ШӘШ§Шұ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ШӯШ§ШөЩ„ Ш§ШІ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ШҜЩҶШҜЩҲЪҜШұШ§Щ… (Dendogram) ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁШ§ Ш§ЩҠЩҶЪ©ЩҮ ШұЩҲШҙвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ ШЁЩҠШҙШӘШұ ЩҲ ШҜЩӮЩҠЩӮвҖҢШӘШұЩҠ ШӘЩҲЩ„ЩҠШҜ Щ…ЩҠвҖҢЪ©ЩҶЩҶШҜ ШЁШұШ§ЩҠ ШӘШӯЩ„ЩҠЩ„ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШ§ Ш¬ШІШҰЩҠШ§ШӘ ЩҫЩҠШҙЩҶЩҮШ§ШҜ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ ЩҲЩ„ЩҠ Ш§ШІ Ш·ШұЩҒЩҠ ЪҶЩҲЩҶ ЩҫЩҠЪҶЩҠШҜЪҜЩҠ Щ…ШӯШ§ШіШЁШ§ШӘЩҠ ШЁШ§Щ„Ш§ЩҠЩҠ ШҜШ§ШұЩҶШҜ ШЁШұШ§ЩҠ Щ…Ш¬Щ…ЩҲШ№ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШІШұЪҜ ШұЩҲШҙвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Щ…ШіШ·Шӯ ЩҫЩҠШҙЩҶЩҮШ§ШҜ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҮЩ…Ш§ЩҶ ЪҜЩҲЩҶЩҮ Ъ©ЩҮ ШЁЩҠШ§ЩҶ ШҙШҜШҢ ШҜШұ ШұЩҲШҙ Ш®ЩҲШҙЩҮ ШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠШҢ ШЁЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ ЩҶЩҮШ§ЩҠЩҠ ШЁШұ Ш§ШіШ§Ші Щ…ЩҠШІШ§ЩҶ Ш№Щ…ЩҲЩ…ЩҠШӘ ШўЩҶЩҮШ§ ШіШ§Ш®ШӘШ§ШұЩҠ ШіЩ„ШіЩ„ЩҮвҖҢ Щ…ШұШ§ШӘШЁЩҠШҢ Щ…Ш№Щ…ЩҲЩ„Ш§ ШЁЩҮ ШөЩҲШұШӘ ШҜШұШ®ШӘЩҠ ЩҶШіШЁШӘ ШҜШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШЁЩҮ Ш§ ЩҠЩҶ ШҜШұШ®ШӘ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ШҜЩҶШҜЩҲЪҜШұШ§Щ… (dendogram) Щ…ЩҠвҖҢЪҜЩҲЩҠЩҶШҜ. ШұЩҲШҙ Ъ©Ш§Шұ ШӘЪ©ЩҶЩҠЪ©ЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮвҖҢЩ…ШұШ§ШӘШЁЩҠ Щ…Ш№Щ…ЩҲЩ„Ш§ ШЁШұ Ш§ШіШ§Ші Ш§Щ„ЪҜЩҲШұЩҠШӘЩ…ЩҮШ§ЩҠ ШӯШұЩҠШөШ§ЩҶЩҮ (Greedy Algorithms) ЩҲ ШЁЩҮЩҠЩҶЪҜЩҠ Щ…ШұШӯЩ„ЩҮвҖҢШ§ЩҠ (stepwise-optimal) Ш§ШіШӘ. ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШұ Ш§ШіШ§Ші ШіШ§Ш®ШӘШ§Шұ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ШӘЩҲЩ„ЩҠШҜЩҠ ШӘЩҲШіШ· ШўЩҶЩҮШ§ Щ…Ш№Щ…ЩҲЩ„Ш§ ШЁЩҮ ШҜЩҲ ШҜШіШӘШ© ШІЩҠШұ ШӘЩӮШіЩҠЩ… Щ…ЩҠвҖҢШҙЩҲЩҶШҜ: 1. ШЁШ§Щ„Ш§ ШЁЩҮ ЩҫШ§ЩҠЩҠЩҶ (Top-Down) ЩҠШ§ ШӘЩӮШіЩҠЩ… Ъ©ЩҶЩҶШҜЩҮ (Divisive): ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ Ш§ШЁШӘШҜШ§ ШӘЩ…Ш§Щ… ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЩҠЪ© Ш®ЩҲШҙЩҮ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ ЩҲ ШіЩҫШі ШҜШұ Ш·ЩҠ ЩҠЪ© ЩҒШұШ§ЩҠЩҶШҜ ШӘЪ©ШұШ§ШұЩҠ ШҜШұ ЩҮШұ Щ…ШұШӯЩ„ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠЩҠ ШҙШЁШ§ЩҮШӘ Ъ©Щ…ШӘШұЩҠ ШЁЩҮ ЩҮЩ… ШҜШ§ШұЩҶШҜ ШЁЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ Щ…Ш¬ШІШ§ЩҠЩҠ ШҙЪ©ШіШӘЩҮ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ ЩҲ Ш§ЩҠЩҶ ШұЩҲШ§Щ„ ШӘШ§ ШұШіЩҠШҜЩҶ ШЁЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠЩҠ Ъ©ЩҮ ШҜШ§ШұШ§ЩҠ ЩҠЪ© Ш№Ш¶ЩҲ ЩҮШіШӘЩҶШҜ Ш§ШҜШ§Щ…ЩҮ ЩҫЩҠШҜШ§ Щ…ЩҠвҖҢЪ©ЩҶШҜ. 2. ЩҫШ§ЩҠЩҠЩҶ ШЁЩҮ ШЁШ§Щ„Ш§ (Bottom-Up) ЩҠШ§ Щ…ШӘШұШ§Ъ©Щ… ШҙЩҲЩҶШҜЩҮ (Agglomerative): ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ Ш§ШЁШӘШҜШ§ ЩҮШұ ШҜШ§ШҜЩҮвҖҢЩҮШ§ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Ш®ЩҲШҙЩҮвҖҢШ§ЩҠ Щ…Ш¬ШІШ§ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ ЩҲ ШҜШұ Ш·ЩҠ ЩҒШұШ§ЩҠЩҶШҜЩҠ ШӘЪ©ШұШ§ШұЩҠ ШҜШұ ЩҮШұ Щ…ШұШӯЩ„ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠЩҠ Ъ©ЩҮ ШҙШЁШ§ЩҮШӘ ШЁЩҠШҙШӘШұЩҠ ШЁШ§ ЩҠЪ©ШҜЩҠЪҜШұ ШЁШ§ ЩҠЪ©ШҜЩҠЪҜШұ ШӘШұЪ©ЩҠШЁ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ ШӘШ§ ШҜШұ ЩҶЩҮШ§ЩҠШӘ ЩҠЪ© Ш®ЩҲШҙЩҮ ЩҲ ЩҠШ§ ШӘШ№ШҜШ§ШҜ Щ…ШҙШ®ШөЩҠ Ш®ЩҲШҙЩҮ ШӯШ§ШөЩ„ ШҙЩҲШҜ. Ш§ШІ Ш§ЩҶЩҲШ§Ш№ Ш§Щ„ЪҜЩҲШұЩҠШӘЩ…ЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ Щ…ШӘШұШ§Ъ©Щ… ШҙЩҲЩҶШҜЩҮ ШұШ§ЩҠШ¬ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ Ш§ШІ Ш§Щ„ЪҜЩҲШұЩҠШӘЩ…ЩҮШ§ЩҠ Single-LinkШҢ Average-Link ЩҲ Complete-Link ЩҶШ§Щ… ШЁШұШҜ. ШӘЩҒШ§ЩҲШӘ Ш§ШөЩ„ЩҠ ШҜШұ ШЁЩҠЩҶ ШӘЩ…Ш§Щ… Ш§ЩҠЩҶ ШұЩҲШҙЩҮШ§ ШЁЩҮ ЩҶШӯЩҲШ© Щ…ШӯШ§ШіШЁШ© ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ Щ…ШұШЁЩҲШ· Щ…ЩҠвҖҢШҙЩҲШҜ. Ъ©ЩҮ ШҜШұ ШЁШ®ШҙЩҮШ§ЩҠ ШЁШ№ШҜ ШЁЩҮ ШӘШҙШұЩҠШӯ ЩҮШұ ЩҠЪ© ЩҫШұШҜШ§Ш®ШӘЩҮ Ш®ЩҲШ§ЩҮШҜ ШҙШҜ. ЩҶЩ…ЩҲЩҶЩҮвҖҢШ§ЩҠ Ш§ШІ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ ШӘЩҒШ§ЩҲШӘ ШЁЩҠЩҶ ШұЩҲШҙЩҮШ§ЩҠ ШЁШ§Щ„Ш§ ШЁЩҮ ЩҫШ§ЩҠЩҠЩҶ ЩҲ ЩҫШ§ЩҠЩҠЩҶ ШЁЩҮ ШЁШ§Щ„Ш§ ШҜШұ ШҙЪ©Щ„ ШІЩҠШұ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ.  ШҙЪ©Щ„ 3: ШӘЩҒШ§ЩҲШӘ ШЁЩҠЩҶ ШұЩҲШҙЩҮШ§ЩҠ ШЁШ§Щ„Ш§ ШЁЩҮ ЩҫШ§ЩҠЩҠЩҶ ШЁШ§ ШұЩҲШҙЩҮШ§ЩҠ ЩҫШ§ЩҠЩҠЩҶ ШЁЩҮ ШЁШ§Щ„Ш§ |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | 3ngineer (Ы°Ыҙ-ЫұЫҙ-ЫұЫіЫ№Ыҙ), 83202200 (Ы°Ыҙ-ЫұЫ¶-ЫұЫіЫёЫ№), Amirmasoud1365 (Ы°Ыё-ЫІЫ·-ЫұЫіЫ№Ы°), dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), farshad1362 (Ы°Ы№-ЫұЫ°-ЫұЫіЫ№Ы°), hamedmehdihamed (ЫұЫІ-ЫІЫ¶-ЫұЫіЫ№Ы°), hamidrezas (Ы°ЫІ-ЫІЫҙ-ЫұЫіЫ№Ы°), mahlla (Ы°Ы№-Ыө-ЫұЫіЫ№Ы°), mozhdeh65 (Ы°Ыё-ЫұЫ№-ЫұЫіЫ№Ы°), redeemer (ЫұЫ°-ЫІ-ЫұЫіЫ№ЫІ), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°) |
|
|
#6 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ШұЩҲШҙ Single-Link
Ш§ЩҠЩҶ ШұЩҲШҙ ЩҠЪ©ЩҠ Ш§ШІ ЩӮШҜЩҠЩ…ЩҠвҖҢШӘШұЩҠЩҶ ЩҲ ШіШ§ШҜЩҮвҖҢШӘШұЩҠЩҶ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Ш§ШіШӘ ЩҲ Ш¬ШІШЎ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ Ш§ЩҶШӯШөШ§ШұЩҠ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢШҙЩҲШҜ. ШЁЩҮ Ш§ЩҠЩҶ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠШҢ ШӘЪ©ЩҶЩҠЪ© ЩҶШІШҜЩҠЪ©ШӘШұЩҠЩҶ ЩҮЩ…ШіШ§ЩҠЩҮ (Nearest Neighbour) ЩҶЩҠШІ ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШЁШұШ§ЩҠ Щ…ШӯШ§ШіШЁШ© ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙШ© A ЩҲ B Ш§ШІ Щ…Ш№ЩҠШ§Шұ ШІЩҠШұ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ:  Ъ©ЩҮ i ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© A ЩҲ j ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜШ© Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© B Щ…ЩҠвҖҢШЁШ§ШҙШҜ. ШҜШұ ЩҲШ§ЩӮШ№ ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮШҢ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ЩҠЪ© Ш№Ш¶ЩҲ Ш§ШІ ЩҠЪ©ЩҠ ШЁШ§ ЩҠЪ© Ш№Ш¶ЩҲ Ш§ШІ ШҜЩҠЪҜШұЩҠ Ш§ШіШӘ. ШҜШұ ШҙЪ©Щ„ ШІЩҠШұ Ш§ЩҠЩҶ Щ…ЩҒЩҮЩҲЩ… ШЁЩҮШӘШұ ЩҶШҙШ§ЩҶвҖҢ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ  ШҙЪ©Щ„ 4: ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ ШҜШұ ШұЩҲШҙ Single-Link ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШҜЩҲ Ш®ЩҲШҙЩҮ 1-1-1- Щ…Ш«Ш§Щ„: ШҜШұ Ш§ЩҠЩҶ ЩӮШіЩ…ШӘ ШіШ№ЩҠ ШҙШҜЩҮ Ш§ШіШӘ ШӘШ§ ШҜШұ Щ…Ш«Ш§Щ„ЩҠ ШЁШ§ ЩҒШұШ¶ ШҜШ§ШҙШӘЩҶ 6 ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ ЩҲ Щ…Ш§ШӘШұЩҠШі ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШўЩҶЩҮШ§ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 1 ЩҶШҙШ§ЩҶвҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘШҢ ЩҶШӯЩҲШ© Ш§Ш№Щ…Ш§Щ„ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Single-Link ШЁЩҮШӘШұ ШӘШҙШұЩҠШӯ ШҙЩҲШҜ Ш¬ШҜЩҲЩ„ 1: Щ…Ш§ШӘШұЩҠШі ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 6 ЩҶЩ…ЩҲЩҶШ© ШҜШ§ШҜЩҮ 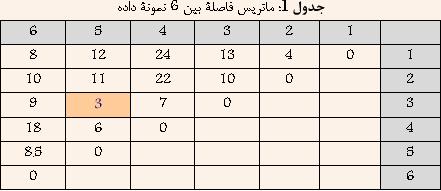 ШҜШұ Ш§ШЁШӘШҜШ§ ЩҮШұ ШҜШ§ШҜЩҮ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЩҠЪ© Ш®ЩҲШҙЩҮ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ ЩҲ ЩҠШ§ЩҒШӘЩҶ ЩҶШІШҜЩҠЪ©ШӘШұЩҠЩҶ Ш®ЩҲШҙЩҮ ШҜШұ ЩҲШ§ЩӮШ№ ЩҠШ§ЩҒШӘЩҶ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШ§Щ„Ш§ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 1 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 3 ЩҲ 5 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 3 ЩҲ ЩҠШ§ 5 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 2 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. 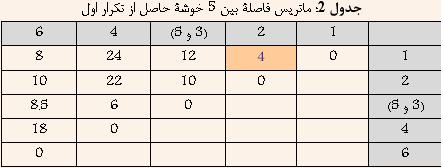 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 2 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 1 ЩҲ 2 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 1 ЩҲ ЩҠШ§ 2 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 3 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. 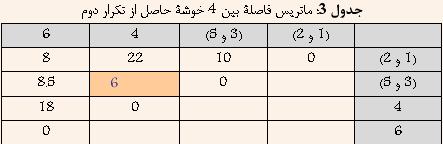 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 3 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (3 ЩҲ 5) ЩҲ 4 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (3 ЩҲ 5) ЩҲ ЩҠШ§ 4 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 4 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. 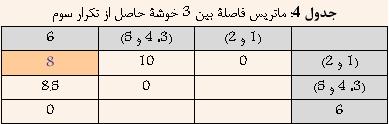 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 4 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (1 ЩҲ 2) ЩҲ 6 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (1 ЩҲ 2) ЩҲ ЩҠШ§ 6 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 5 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШҜШұ ЩҶЩҮШ§ЩҠШӘ Ш§ЩҠЩҶ ШҜЩҲ Ш®ЩҲвҖҢШҙШ© ШӯШ§ШөЩ„ Ш§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ ШҜЩҶШҜЩҲЪҜШұШ§Щ… ШҙЪ©Щ„ 5 ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШҙЪ©Щ„ 5: ШҜЩҶШҜЩҲЪҜШұШ§Щ… Щ…Ш«Ш§Щ„ Single-Link |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | 3ngineer (Ы°Ыҙ-ЫұЫҙ-ЫұЫіЫ№Ыҙ), dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), farshad1362 (Ы°Ы№-ЫұЫ°-ЫұЫіЫ№Ы°), hamidrezas (Ы°ЫІ-ЫІЫҙ-ЫұЫіЫ№Ы°), redeemer (ЫұЫ°-ЫІ-ЫұЫіЫ№ЫІ), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°) |
|
|
#7 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ШұЩҲШҙ Complete-Link
Ш§ЩҠЩҶ ШұЩҲШҙ ЩҮЩ…Ш§ЩҶЩҶШҜ Single-Link Ш¬ШІШЎ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ Ш§ЩҶШӯШөШ§ШұЩҠ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢШҙЩҲШҜ. ШЁЩҮ Ш§ЩҠЩҶ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠШҢ ШӘЪ©ЩҶЩҠЪ© ШҜЩҲШұШӘШұЩҠЩҶ ЩҮЩ…ШіШ§ЩҠЩҮ (furthest Neighbour) ЩҶЩҠШІ ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШЁШұШ§ЩҠ Щ…ШӯШ§ШіШЁШ© ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙШ© A ЩҲ B Ш§ШІ Щ…Ш№ЩҠШ§Шұ ШІЩҠШұ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ:  Ъ©ЩҮ i ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© A ЩҲ j ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜШ© Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© B Щ…ЩҠвҖҢШЁШ§ШҙШҜ. ШҜШұ ЩҲШ§ЩӮШ№ ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ЩҠЪ© Ш№Ш¶ЩҲ Ш§ШІ ЩҠЪ©ЩҠ ШЁШ§ ЩҠЪ© Ш№Ш¶ЩҲ Ш§ШІ ШҜЩҠЪҜШұЩҠ Ш§ШіШӘ. ШҜШұ ШҙЪ©Щ„ ШІЩҠШұ Ш§ЩҠЩҶ Щ…ЩҒЩҮЩҲЩ… ШЁЩҮШӘШұ ЩҶШҙШ§ЩҶвҖҢ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШҙЪ©Щ„ 6: ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ ШҜШұ ШұЩҲШҙ Complete-Link ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШҜЩҲ Ш®ЩҲШҙЩҮ. Щ…Ш«Ш§Щ„: ШҜШұ Ш§ЩҠЩҶ ЩӮШіЩ…ШӘ ШіШ№ЩҠ ШҙШҜЩҮ Ш§ШіШӘ ШӘШ§ ШҜШұ Щ…Ш«Ш§Щ„ЩҠ ШЁШ§ ЩҒШұШ¶ ШҜШ§ШҙШӘЩҶ 6 ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ ЩҲ Щ…Ш§ШӘШұЩҠШі ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШўЩҶЩҮШ§ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 6 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘШҢ ЩҶШӯЩҲШ© Ш§Ш№Щ…Ш§Щ„ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Complete-Link ШЁЩҮШӘШұ ШӘШҙШұЩҠШӯ ШҙЩҲШҜ. 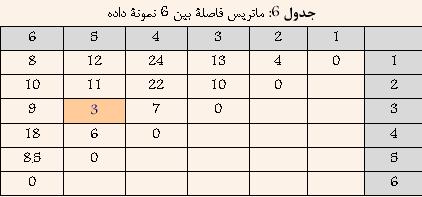 ШҜШұ Ш§ШЁШӘШҜШ§ ЩҮШұ ШҜШ§ШҜЩҮ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЩҠЪ© Ш®ЩҲШҙЩҮ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ ЩҲ ЩҠШ§ЩҒШӘЩҶ ЩҶШІШҜЩҠЪ©ШӘШұЩҠЩҶ Ш®ЩҲШҙЩҮ ШҜШұ ЩҲШ§ЩӮШ№ ЩҠШ§ЩҒШӘЩҶ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШ§Щ„Ш§ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 6 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 3 ЩҲ 5 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 3 ЩҲ ЩҠШ§ 5 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 7 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. 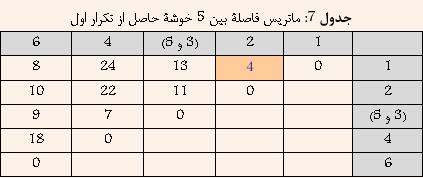 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 7 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 1 ЩҲ 2 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 1 ЩҲ ЩҠШ§ 2 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 8 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. 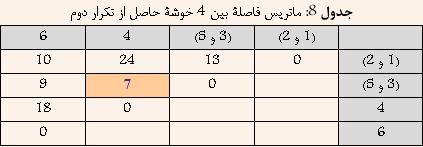 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 8 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (3 ЩҲ 5) ЩҲ 4 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (3 ЩҲ 5) ЩҲ ЩҠШ§ 4 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 9 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. 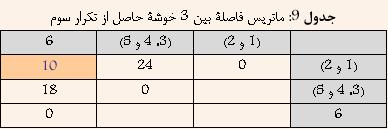 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 9 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (1 ЩҲ 2) ЩҲ 6 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (1 ЩҲ 2) ЩҲ ЩҠШ§ 6 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 10 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШҜШұ ЩҶЩҮШ§ЩҠШӘ Ш§ЩҠЩҶ ШҜЩҲ Ш®ЩҲвҖҢШҙШ© ШӯШ§ШөЩ„ Ш§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ ШҜЩҶШҜЩҲЪҜШұШ§Щ… ШҙЪ©Щ„ 7 ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШҙЪ©Щ„ 7: ШҜЩҶШҜЩҲЪҜШұШ§Щ… Щ…Ш«Ш§Щ„ Complete-Link |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | 3ngineer (Ы°Ыҙ-ЫұЫҙ-ЫұЫіЫ№Ыҙ), dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), farshad1362 (Ы°Ы№-ЫұЫ°-ЫұЫіЫ№Ы°), hamedmehdihamed (ЫұЫІ-ЫІЫ¶-ЫұЫіЫ№Ы°), redeemer (ЫұЫ°-ЫІ-ЫұЫіЫ№ЫІ), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°) |
|
|
#8 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ШұЩҲШҙ Average-Link
Ш§ЩҠЩҶ ШұЩҲШҙ ЩҮЩ…Ш§ЩҶЩҶШҜ Single-Link Ш¬ШІШЎ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ Ш§ЩҶШӯШөШ§ШұЩҠ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢШҙЩҲШҜ. Ш§ШІ ШўЩҶШ¬Ш§ Ъ©ЩҮ ЩҮШұ ШҜЩҲ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Single-link ЩҲ Complete-link ШЁШҙШҜШӘ ШЁЩҮ ЩҶЩҲЩҠШІ ШӯШіШ§Ші Щ…ЩҠвҖҢШЁШ§ШҙШҜШҢ Ш§ЩҠЩҶ ШұЩҲШҙ Ъ©ЩҮ Щ…ШӯШ§ШіШЁШ§ШӘ ШЁЩҠШҙШӘШұЩҠ ШҜШ§ШұШҜШҢ ЩҫЩҠШҙЩҶЩҮШ§ШҜ ШҙШҜ. ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШЁШұШ§ЩҠ Щ…ШӯШ§ШіШЁШ© ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙШ© A ЩҲ B Ш§ШІ Щ…Ш№ЩҠШ§Шұ ШІЩҠШұ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ:  Ъ©ЩҮ i ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© A ЩҲ j ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜШ© Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© B Щ…ЩҠвҖҢШЁШ§ШҙШҜ. ЩҲ NA ШӘШ№ШҜШ§ШҜ Ш§Ш№Ш¶Ш§ШЎ Ш®ЩҲШҙШ© A ЩҲ NB ШӘШ№ШҜШ§ШҜ Ш§Ш№Ш¶Ш§ШЎ Ш®ЩҲШҙШ© B Ш§ШіШӘ. ШҜШұ ЩҲШ§ЩӮШ№ ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙШҢ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШӘЩ…Ш§Щ… Ш§Ш№Ш¶Ш§ШЎ ЩҠЪ©ЩҠ ШЁШ§ ШӘЩ…Ш§Щ… Ш§Ш№Ш¶Ш§ШЎ ШҜЩҠЪҜШұЩҠ Ш§ШіШӘ. ШҜШұ ШҙЪ©Щ„ ШІЩҠШұ Ш§ЩҠЩҶ Щ…ЩҒЩҮЩҲЩ… ШЁЩҮШӘШұ ЩҶШҙШ§ЩҶвҖҢ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ  ШҙЪ©Щ„ 8: ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ ШҜШұ ШұЩҲШҙ Average-Link ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШҜЩҲ Ш®ЩҲШҙЩҮ Щ…Ш«Ш§Щ„: ШҜШұ Ш§ЩҠЩҶ ЩӮШіЩ…ШӘ ШіШ№ЩҠ ШҙШҜЩҮ Ш§ШіШӘ ШӘШ§ ШҜШұ Щ…Ш«Ш§Щ„ЩҠ ШЁШ§ ЩҒШұШ¶ ШҜШ§ШҙШӘЩҶ 6 ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ ЩҲ Щ…Ш§ШӘШұЩҠШі ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШўЩҶЩҮШ§ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 11 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘШҢ ЩҶШӯЩҲШ© Ш§Ш№Щ…Ш§Щ„ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Average-Link ШЁЩҮШӘШұ ШӘШҙШұЩҠШӯ ШҙЩҲШҜ 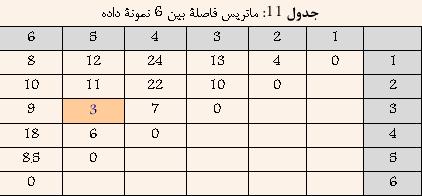 ШҜШұ Ш§ШЁШӘШҜШ§ ЩҮШұ ШҜШ§ШҜЩҮ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЩҠЪ© Ш®ЩҲШҙЩҮ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ ЩҲ ЩҠШ§ЩҒШӘЩҶ ЩҶШІШҜЩҠЪ©ШӘШұЩҠЩҶ Ш®ЩҲШҙЩҮ ШҜШұ ЩҲШ§ЩӮШ№ ЩҠШ§ЩҒШӘЩҶ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШ§Щ„Ш§ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 11 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 3 ЩҲ 5 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 3 ЩҲ 5 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 12 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 12 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 1 ЩҲ 2 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 1 ЩҲ ЩҠШ§ 2 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 13 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ 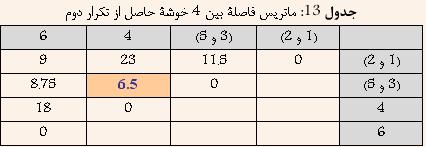 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 13 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (3 ЩҲ 5) ЩҲ 4 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (3 ЩҲ 5) ЩҲ ЩҠШ§ 4 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 14 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. 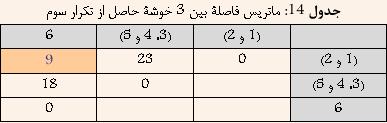 ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 14 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (1 ЩҲ 2) ЩҲ 6 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁЩҠШҙШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (1 ЩҲ 2) ЩҲ ЩҠШ§ 6 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 15 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШҜШұ ЩҶЩҮШ§ЩҠШӘ Ш§ЩҠЩҶ ШҜЩҲ Ш®ЩҲвҖҢШҙШ© ШӯШ§ШөЩ„ Ш§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ ШҜЩҶШҜЩҲЪҜШұШ§Щ… ШҙЪ©Щ„ 9 ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.  ШҙЪ©Щ„ 9: ШҜЩҶШҜЩҲЪҜШұШ§Щ… Щ…Ш«Ш§Щ„ Average-Link |
|
|

|
|
|
#9 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
ШҜЩҠЪҜШұ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮ ШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ
*Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ШұЩҲШҙ Group Average Link: Ш§ЩҠЩҶ ШұЩҲШҙ ЩҮЩ…Ш§ЩҶЩҶШҜ Single-Link Ш¬ШІШЎ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ Ш§ЩҶШӯШөШ§ШұЩҠ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢШҙЩҲШҜ. [Webb] ШЁЩҮ Ш§ЩҠЩҶ ШұЩҲШҙ Centriod Distance ЩҶЩҠШІ ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШЁШұШ§ЩҠ Щ…ШӯШ§ШіШЁШ© ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙШ© A ЩҲ B Ш§ШІ Щ…Ш№ЩҠШ§Шұ ШІЩҠШұ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ:  Ъ©ЩҮ Xi ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© AШҢ Xj ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜШ© Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© BШҢ NA ШӘШ№ШҜШ§ШҜ Ш§Ш№Ш¶Ш§ШЎ Ш®ЩҲШҙШ©A ЩҲ NB ШӘШ№ШҜШ§ШҜ Ш§Ш№Ш¶Ш§ШЎ Ш®ЩҲШҙШ© B Ш§ШіШӘ. ШҜШұ ЩҲШ§ЩӮШ№ ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙШҢ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШЁШұШҜШ§Шұ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶЩҗ ШӘЩ…Ш§Щ… Ш§Ш№Ш¶Ш§ШЎ ЩҠЪ©ЩҠ ШЁШ§ ШЁШұШҜШ§ШұЩҗ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶЩҗ ШӘЩ…Ш§Щ… Ш§Ш№Ш¶Ш§ШЎ ШҜЩҠЪҜШұЩҠ Ш§ШіШӘ. ШҜШұ ШҙЪ©Щ„ F4 Ш§ЩҠЩҶ Щ…ЩҒЩҮЩҲЩ… ШЁЩҮШӘШұ ЩҶШҙШ§ЩҶвҖҢ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. * Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ШұЩҲШҙ Median Distance: Ш§ЩҠЩҶ ШұЩҲШҙ ЩҶЩҠШІ ЩҮЩ…Ш§ЩҶЩҶШҜ Single-Link Ш¬ШІШЎ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ Ш§ЩҶШӯШөШ§ШұЩҠ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢШҙЩҲШҜ. ШҜШұ ШұЩҲШҙ Group Average Link Ш§ЪҜШұ ЩҠЩ… Ш®ЩҲШҙШ© Ъ©ЩҲЪҶЪ© ШЁШ§ ЩҠЪ© Ш®ЩҲШҙШ© ШЁШІШұЪҜ ШӘШұЪ©ЩҠШЁ ШҙЩҲШҜ ЩҶЩӮШ·Ш© Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ Ш®ЩҲШҙШ© ШӯШ§ШөЩ„ ЩҶЩӮШ·ЩҮвҖҢШ§ЩҠ ЩҶШІШҜЩҠЪ© Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ Ш®ЩҲШҙШ© ШЁШІШұЪҜШӘШұ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ Ъ©ЩҮ ШҜШұ ШЁШ№Ш¶ЩҠ Ш§ШІ Ъ©Ш§ШұШЁШұШҜЩҮШ§ ЪҶЩҶШҜШ§ЩҶ Щ…Ш·Щ„ЩҲШЁ ЩҶЩҠШіШӘ. ШЁШҜЩҠЩҶ Щ…ЩҶШёЩҲШұ Ш§ЩҠЩҶ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҫЩҠШҙЩҶЩҮШ§ШҜ ШҙШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ Щ…ШҙЪ©Щ„ Щ…Ш°Ъ©ЩҲШұ ШұШ§ ЩҶШҜШ§ШұШҜ. ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ Ш§ШІ Щ…ЩҠШ§ЩҶШ© ЩҶЩӮШ§Ш· ЩҠЪ© Ш®ЩҲШҙЩҮ ШЁЩҮвҖҢ Ш№ЩҶЩҲШ§ЩҶ Щ…ШұЪ©ШІ Ш«ЩӮЩ„ ШўЩҶ Ш®ЩҲШҙЩҮ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ.  ШҙЪ©Щ„ 10: ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ ШҜШұ ШұЩҲШҙ Group Average Link ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ЩҒШ§ШөЩ„ЩҮ ШЁЩҠЩҶ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ ЩҶЩӮШ§Ш· ШҜЩҲ Ш®ЩҲШҙЩҮ * Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ШұЩҲШҙ Ward: Ш§ЩҠЩҶ ШұЩҲШҙ ЩҶЩҠШІ ЩҮЩ…Ш§ЩҶЩҶШҜ Single-Link Ш¬ШІШЎ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ Ш§ЩҶШӯШөШ§ШұЩҠ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢШҙЩҲШҜ. ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢвҖҢШЁЩҶШҜЩҠ ШЁШұШ§ЩҠ Ъ©Ш§ЩҮШҙ ШӘЩ„ЩҒШ§ШӘ ЩҶШ§ШҙЩҠ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШҜЩҲШұ Ш§ЩҒШӘШ§ШҜЩҮ (Outlier) Ш§ШІ Щ…Ш№ЩҠШ§ШұЩҠ Ш¬ШҜЩҠШҜ ШЁШұШ§ЩҠ Щ…ШӯШ§ШіШЁШ© Ш№ШҜЩ…вҖҢШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢЪ©ЩҶШҜ. ШҜШұ ШұЩҲШҙ Ward's Ш§ШІ Щ…Ш¬Щ…ЩҲШ№ Щ…ШұШЁШ№Ш§ШӘ ШӘЩҒШ§Ш¶Щ„ ЩҮШұ ШҜШ§ШҜЩҮ Ш§ШІ ЩҠЪ© Ш®ЩҲШҙЩҮ ШЁШ§ ШЁШұШҜШ§Шұ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ ШўЩҶ Ш®ЩҲШҙЩҮ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Щ…Ш№ЩҠШ§ШұЩҠ ШЁШұШ§ЩҠ ШіЩҶШ¬Шҙ ЩҠЪ© Ш®ЩҲШҙШ© Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. Ш§Щ„ЪҜЩҲШұЩҠШӘЩ… ШІЩҠШұ ШұШ§ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ ШЁШұШ§ЩҠ ШұЩҲШҙ Ward ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘ. 1. Ш§ШЁШӘШҜШ§ ЩҮШұ ШҜШ§ШҜЩҮ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЩҠЪ© Ш®ЩҲШҙЩҮ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. 2. ШЁЩҮ Ш§ШІШ§ШЎ ШӘЩ…Ш§Щ… Ш¬ЩҒШӘ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ Щ…Щ…Ъ©ЩҶ Ш§ШІ Щ…Ш¬Щ…ЩҲШ№Ш© Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШўЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮвҖҢШ§ЩҠ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ Щ…ШұШЁШ№Ш§ШӘ ШӘЩҒШ§Ш¶Щ„ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ Ш®ЩҲШҙШ© ШӯШ§ШөЩ„ Ш§ШІ Ш§Ш¬ШӘЩ…Ш§Ш№ ШўЩҶЩҮШ§ ШЁШ§ ШЁШұШҜШ§Шұ Щ…ЩҠШ§ЩҶЪҜЩҠЩҶ Ш®ЩҲШҙШ© ШӯШ§ШөЩ„ Ъ©Щ…ЩҠЩҶЩҮ ШЁШ§ШҙШҜШҢ Ш§ЩҶШӘШ®Ш§ШЁ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. 3. ШҜЩҲ Ш®ЩҲШҙШ© Ш§ЩҶШӘШ®Ш§ШЁ ШҙШҜЩҮ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. 4. ШӘШ§ ШІЩ…Ш§ЩҶЩҠ Ъ©ЩҮ ШӘШ№ШҜШ§ШҜ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁЩҮ ШӘШ№ШҜШ§ШҜ Щ…ЩҲШұШҜ ЩҶШёШұ ЩҶШұШіЩҠШҜЩҮ Ш§ШіШӘШҢ Щ…ШұШ§ШӯЩ„ iiШҢ iii ЩҲ iv ШӘЪ©ШұШ§Шұ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | 3ngineer (Ы°Ыҙ-ЫұЫҙ-ЫұЫіЫ№Ыҙ), atefeh.esmaili (Ы°Ы№-Ыі-ЫұЫіЫёЫ№), dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°) |
|
|
#10 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Ш§Щ„ЪҜЩҲШұЩҠШӘЩ… Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҫШ§ЩҠЩҠЩҶ ШЁЩҮ ШЁШ§Щ„Ш§ЩҠ Ш№Щ…ЩҲЩ…ЩҠ
Ш§ШәЩ„ШЁ Ш§Щ„ЪҜЩҲШұЩҠШӘЩ…ЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ШұШ§ ШЁЩҮ ЩҶШӯЩҲЩҠ Щ…ЩҠвҖҢШӘЩҲШ§ЩҶ ЪҜШіШӘШұШҙ ЩҠШ§ЩҒШӘШ© Ш§Щ„ЪҜЩҲШұЩҠШӘЩ… Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Single-Link ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘ. ШӘЩҒШ§ЩҲШӘ ШұЩҲШҙЩҮШ§ЩҠ Щ…Ш®ШӘЩ„ЩҒ ШҜШұ ЩҶШӯЩҲШ© Щ…ШӯШ§ШіШЁШ© Щ…Ш§ШӘШұЩҠШі ШӘШҙШ§ШЁЩҮ ЩҠШ§ Ш№ШҜЩ… ШӘШҙШ§ШЁЩҮ (Dissimilaritye) ШўЩҶЩҮШ§ Ш§ШіШӘ. ЩҒШұЩ…ЩҲЩ„ЩҠ ШЁШ§ШІЪҜШҙШӘЩҠ ШЁЩҮ ЩҶШ§Щ… ЩҒШұЩ…ЩҲЩ„ Lance-Williams ШӘШ№ШұЩҠЩҒ ШҙШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ Ш№ШҜЩ…вҖҢШӘШҙШ§ШЁЩҮ ШЁЩҠЩҶ Ш®ЩҲШҙШ© k ЩҲ Ш®ЩҲШҙШ© ШӯШ§ШөЩ„ Ш§ШІ ЩҫЩҠЩҲЩҶШҜ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ i ЩҲ j ШұШ§ ШЁЩҠШ§ЩҶ Щ…ЩҠвҖҢЪ©ЩҶШҜ:  Ъ©ЩҮ ЩҫШ§ШұШ§Щ…ШӘШұЩҮШ§ЩҠ aiШҢ b ЩҲ c ШЁЩҠШ§ЩҶ Ъ©ЩҶЩҶШҜШ© ЩҶЩҲШ№ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ЩҮШіШӘЩҶШҜ ЩҲ ШҜШұ Ш¬ШҜЩҲЩ„ 16 Щ…ЩӮШ§ШҜЩҠШұ Щ…ШұШЁЩҲШ· ШЁЩҮ ЪҶЩҶШҜ ШұЩҲШҙ ШўЩҲШұШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ: 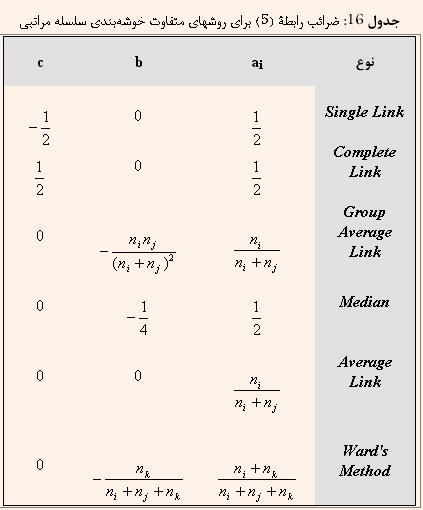
|
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | 83202200 (Ы°Ыҙ-ЫұЫ¶-ЫұЫіЫёЫ№), aimaryam (Ы°Ыө-ЫұЫ°-ЫұЫіЫёЫ№), atefeh.esmaili (Ы°Ы№-ЫІ-ЫұЫіЫёЫ№), dr_bijan (Ы°Ы№-ЫІЫі-ЫұЫіЫ№ЫІ), Faa916 (Ы°Ыё-Ы¶-ЫұЫіЫ№Ы¶), hamedmehdihamed (ЫұЫІ-ЫІЫ¶-ЫұЫіЫ№Ы°), mardin200 (ЫұЫІ-Ыө-ЫұЫіЫёЫё), reza_kh (Ы°Ыё-ЫұЫ°-ЫұЫіЫ№Ы°), Ш§Щ„ЩҮЩҮsh (ЫұЫ°-ЫұЫІ-ЫұЫіЫёЫ№) |
 |
«
ШўЩ…ЩҲШІШҙ ЩҶШұЩ… Ш§ЩҒШІШ§Шұ ШҙШЁЫҢЩҮ ШіШ§ШІЫҢ ЩҶШӘ Щ„ЩҲЪҜЩҲ
|
ЩҶШӯЩҲЩҮ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ШҙШ§Ш®Шө ЩҮШ§ЫҢ Ш§Ш№ШӘШЁШ§ШұШіЩҶШ¬ЫҢ ШҜШұ Щ…ШӘЩ„ШЁ
»
| ЩғШ§ШұШЁШұШ§ЩҶ ШҜШұ ШӯШ§Щ„ ШҜЩҠШҜЩҶ ШӘШ§ЩҫЩҠЪ©: 1 (0 Ш№Ш¶ЩҲ ЩҲ 1 Щ…ЩҮЩ…Ш§ЩҶ) | |
|
|
ШІЩ…Ш§ЩҶ Щ…ШӯЩ„ЩҠ ШҙЩ…Ш§ ШЁШ§ ШӘЩҶШёЩҠЩ… GMT +3.5 ЩҮЩ… Ш§Ъ©ЩҶЩҲЩҶ Ы°Ыұ:ЫөЫё ЩӮШЁЩ„ Ш§ШІ ШёЩҮШұ Щ…ЩҠШЁШ§ШҙШҜ.






 Linear Mode
Linear Mode







