خوشهبندي با روش Average-Link
اين روش همانند Single-Link جزء روشهاي خوشهبندي سلسله مراتبي و انحصاري محسوب ميشود. از آنجا که هر دو روش خوشهبندي Single-link و Complete-link بشدت به نويز حساس ميباشد، اين روش که محاسبات بيشتري دارد، پيشنهاد شد. در اين روش براي محاسبة شباهت بين دو خوشة A و B از معيار زير استفاده ميشود:

که i يک نمونه داده متعلق به خوشة A و j يک نمونه دادة متعلق به خوشة B ميباشد. و NA تعداد اعضاء خوشة A و NB تعداد اعضاء خوشة B است. در واقع در اين روش، شباهت بين دو خوشه ميانگين فاصلة بين تمام اعضاء يکي با تمام اعضاء ديگري است. در شکل زير اين مفهوم بهتر نشان داده شده است

شکل 8: شباهت بين دو خوشه در روش Average-Link برابر است با ميانگين فاصلة بين دادههاي دو خوشه
مثال: در اين قسمت سعي شده است تا در مثالي با فرض داشتن 6 نمونه داده و ماتريس فاصلة بين آنها که در جدول 11 نشان داده شده است، نحوة اعمال روش خوشهبندي Average-Link بهتر تشريح شود
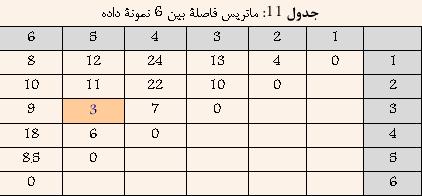
در ابتدا هر داده به عنوان يک خوشه در نظر گرفته ميشود و يافتن نزديکترين خوشه در واقع يافتن کمترين فاصلة بين دادههاي بالا خواهد بود. با توجه به جدول 11 مشخص است که دادههاي 3 و 5 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با ميانگين فاصلة بين 3 و 5 از ساير خوشهها. نتيجه در جدول 12 نشان داده شده است.

با توجه به جدول 12 مشخص است که دادههاي 1 و 2 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين 1 و يا 2 از ساير خوشهها. نتيجه در جدول 13 نشان داده شده است
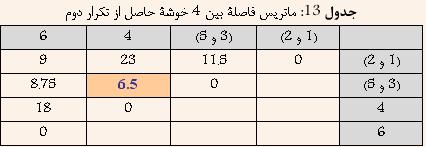
با توجه به جدول 13 مشخص است که خوشههاي (3 و 5) و 4 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين (3 و 5) و يا 4 از ساير خوشهها. نتيجه در جدول 14 نشان داده شده است.
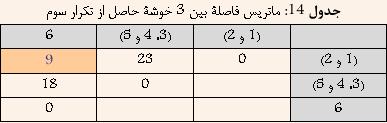
با توجه به جدول 14 مشخص است که خوشههاي (1 و 2) و 6 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين (1 و 2) و يا 6 از ساير خوشهها. نتيجه در جدول 15 نشان داده شده است.

در نهايت اين دو خوشة حاصل ا هم ترکيب ميشوند. نتيجه در دندوگرام شکل 9 نشان داده شده است.

شکل 9: دندوگرام مثال Average-Link