Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШЁШ§ ШұЩҲШҙ Single-Link
Ш§ЩҠЩҶ ШұЩҲШҙ ЩҠЪ©ЩҠ Ш§ШІ ЩӮШҜЩҠЩ…ЩҠвҖҢШӘШұЩҠЩҶ ЩҲ ШіШ§ШҜЩҮвҖҢШӘШұЩҠЩҶ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Ш§ШіШӘ ЩҲ Ш¬ШІШЎ ШұЩҲШҙЩҮШ§ЩҠ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ ШіЩ„ШіЩ„ЩҮ Щ…ШұШ§ШӘШЁЩҠ ЩҲ Ш§ЩҶШӯШөШ§ШұЩҠ Щ…ШӯШіЩҲШЁ Щ…ЩҠвҖҢШҙЩҲШҜ. ШЁЩҮ Ш§ЩҠЩҶ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠШҢ ШӘЪ©ЩҶЩҠЪ© ЩҶШІШҜЩҠЪ©ШӘШұЩҠЩҶ ЩҮЩ…ШіШ§ЩҠЩҮ (Nearest Neighbour) ЩҶЩҠШІ ЪҜЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ. ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШЁШұШ§ЩҠ Щ…ШӯШ§ШіШЁШ© ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙШ© A ЩҲ B Ш§ШІ Щ…Ш№ЩҠШ§Шұ ШІЩҠШұ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ:

Ъ©ЩҮ i ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© A ЩҲ j ЩҠЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜШ© Щ…ШӘШ№Щ„ЩӮ ШЁЩҮ Ш®ЩҲШҙШ© B Щ…ЩҠвҖҢШЁШ§ШҙШҜ. ШҜШұ ЩҲШ§ЩӮШ№ ШҜШұ Ш§ЩҠЩҶ ШұЩҲШҙ ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮШҢ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ЩҠЪ© Ш№Ш¶ЩҲ Ш§ШІ ЩҠЪ©ЩҠ ШЁШ§ ЩҠЪ© Ш№Ш¶ЩҲ Ш§ШІ ШҜЩҠЪҜШұЩҠ Ш§ШіШӘ. ШҜШұ ШҙЪ©Щ„ ШІЩҠШұ Ш§ЩҠЩҶ Щ…ЩҒЩҮЩҲЩ… ШЁЩҮШӘШұ ЩҶШҙШ§ЩҶвҖҢ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ

ШҙЪ©Щ„ 4: ШҙШЁШ§ЩҮШӘ ШЁЩҠЩҶ ШҜЩҲ Ш®ЩҲШҙЩҮ ШҜШұ ШұЩҲШҙ Single-Link ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШҜЩҲ Ш®ЩҲШҙЩҮ
1-1-1- Щ…Ш«Ш§Щ„: ШҜШұ Ш§ЩҠЩҶ ЩӮШіЩ…ШӘ ШіШ№ЩҠ ШҙШҜЩҮ Ш§ШіШӘ ШӘШ§ ШҜШұ Щ…Ш«Ш§Щ„ЩҠ ШЁШ§ ЩҒШұШ¶ ШҜШ§ШҙШӘЩҶ 6 ЩҶЩ…ЩҲЩҶЩҮ ШҜШ§ШҜЩҮ ЩҲ Щ…Ш§ШӘШұЩҠШі ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШўЩҶЩҮШ§ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 1 ЩҶШҙШ§ЩҶвҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘШҢ ЩҶШӯЩҲШ© Ш§Ш№Щ…Ш§Щ„ ШұЩҲШҙ Ш®ЩҲШҙЩҮвҖҢШЁЩҶШҜЩҠ Single-Link ШЁЩҮШӘШұ ШӘШҙШұЩҠШӯ ШҙЩҲШҜ
Ш¬ШҜЩҲЩ„ 1: Щ…Ш§ШӘШұЩҠШі ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 6 ЩҶЩ…ЩҲЩҶШ© ШҜШ§ШҜЩҮ
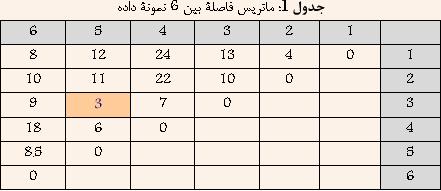
ШҜШұ Ш§ШЁШӘШҜШ§ ЩҮШұ ШҜШ§ШҜЩҮ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЩҠЪ© Ш®ЩҲШҙЩҮ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЩҠвҖҢШҙЩҲШҜ ЩҲ ЩҠШ§ЩҒШӘЩҶ ЩҶШІШҜЩҠЪ©ШӘШұЩҠЩҶ Ш®ЩҲШҙЩҮ ШҜШұ ЩҲШ§ЩӮШ№ ЩҠШ§ЩҒШӘЩҶ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ ШЁШ§Щ„Ш§ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 1 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 3 ЩҲ 5 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 3 ЩҲ ЩҠШ§ 5 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 2 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.
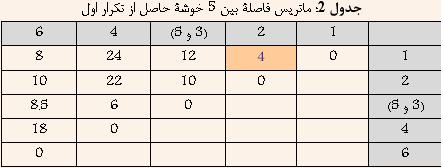
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 2 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ ШҜШ§ШҜЩҮвҖҢЩҮШ§ЩҠ 1 ЩҲ 2 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ 1 ЩҲ ЩҠШ§ 2 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 3 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.
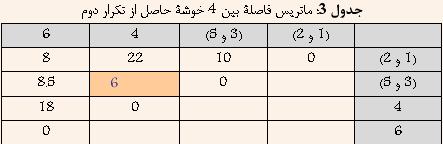
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 3 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (3 ЩҲ 5) ЩҲ 4 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (3 ЩҲ 5) ЩҲ ЩҠШ§ 4 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 4 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.
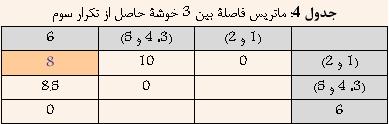
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш¬ШҜЩҲЩ„ 4 Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ЩҠ (1 ЩҲ 2) ЩҲ 6 Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„ЩҮ ШұШ§ ШҜШ§ШұШ§ ЩҮШіШӘЩҶШҜ. ЩҲ ШҜШұ ЩҶШӘЩҠШ¬ЩҮ ШўЩҶЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Ъ©ШұШҜЩҮ ЩҲ Ш®ЩҲШҙШ© Ш¬ШҜЩҠШҜЩҠ ШӯШ§ШөЩ„ Щ…ЩҠвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„Ш© ШўЩҶ Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ъ©Щ…ШӘШұЩҠЩҶ ЩҒШ§ШөЩ„Ш© ШЁЩҠЩҶ (1 ЩҲ 2) ЩҲ ЩҠШ§ 6 Ш§ШІ ШіШ§ЩҠШұ Ш®ЩҲШҙЩҮвҖҢЩҮШ§. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ 5 ЩҶШҙШ§ЩҶ вҖҢШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.

ШҜШұ ЩҶЩҮШ§ЩҠШӘ Ш§ЩҠЩҶ ШҜЩҲ Ш®ЩҲвҖҢШҙШ© ШӯШ§ШөЩ„ Ш§ ЩҮЩ… ШӘШұЪ©ЩҠШЁ Щ…ЩҠвҖҢШҙЩҲЩҶШҜ. ЩҶШӘЩҠШ¬ЩҮ ШҜШұ ШҜЩҶШҜЩҲЪҜШұШ§Щ… ШҙЪ©Щ„ 5 ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.

ШҙЪ©Щ„ 5: ШҜЩҶШҜЩҲЪҜШұШ§Щ… Щ…Ш«Ш§Щ„ Single-Link