 |
انجمن را در گوگل محبوب کنيد :
|
|||||||
 |
| تبليغات سايت | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  |
|
|
LinkBack | ابزارهاي تاپيک | نحوه نمايش |
|
|
#11 (لینک دائم) |
|
Administrator
 |
روش خوشهبندي K-Means (C-Means يا C-Centeriod)
اين روش عليرغم سادگي آن يک روش پايه براي بسياري از روشهاي خوشهبندي ديگر (مانند خوشهبندي فازي) محسوب ميشود. اين روش روشي انحصاري و مسطح محسوب ميشود.[1] براي اين الگوريتم شکلهاي مختلفي بيان شده است. ولي همة آنها داراي روالي تکراري هستند که براي تعدادي ثابت از خوشهها سعي در تخمين موارد زير دارند: · بدست آوردن نقاطي به عنوان مراکز خوشهها اين نقاط در واقع همان ميانگين نقاط متعلق به هر خوشه هستند. · نسبت دادن هر نمونه داده به يک خوشه که آن داده کمترين فاصله تا مرکز آن خوشه را دارا باشد. در نوع سادهاي از اين روش ابتدا به تعداد خوشههاي مورد نياز نقاطي به صورت تصادفي انتخاب ميشود. سپس در دادهها با توجه با ميزان نزديکي (شباهت) به يکي از اين خوشهها نسبت داده ميشوند و بدين ترتيب خوشههاي جديدي حاصل ميشود. با تکرار همين روال ميتوان در هر تکرار با ميانگينگيري از دادهها مراکز جديدي براي آنها محاسبه کرد و مجدادأ دادهها را به خوشههاي جديد نسبت داد. اين روند تا زماني ادامه پيدا ميکند که ديگر تغييري در دادهها حاصل نشود. تابع زير به عنوان تابع هدف مطرح است.  که ║║ معيار فاصلة بين نقاط و cj مرکز خوشة j ام است. الگوريتم زير الگوريتم پايه براي اين روش محسوب ميشود: 1. در ابتدا K نقطه به عنوان به نقاط مراکز خوشهها انتخاب ميشوند. 2. هر نمونه داده به خوشهاي که مرکز آن خوشه کمترين فاصله تا آن داده را داراست، نسبت داده ميشود. 3. پس تعلق تمام دادهها به يکي از خوشهها براي هر خوشه يک نقطه جديد به عنوان مرکز محاسبه ميشود. (ميانگين نقاط متعلق به هر خوشه) 4. مراحل 2 و 3 تکرار ميشوند تا زماني که ديگر هيچ تغييري در مراکز خوشهها حاصل نشود. مثالي براي روش خوشهبندي K-Means: در شکل زير نحوة اعمال اين الگوريتم خوشهبندي روي يک مجموعه داده که شامل دو گروه داده است نشان داده شده است. يک گروه از دادهها با ستاره و گروه ديگر با دايره مشخص شده اند(a). در مرحله اول نقطهاي به عنوان مرکز خوشهها انتخاب شده اند که با رنگ قرمز نشانداده شده اند(b). سپس در مرحله دوم هر يک از نمونه دادهها به يکي از اين دو خوشه نسبت داده شده است و براي هر دسته جديد مرکزي جديد محاسبه شده سات که در قسمت c نشان داده شده اند. اين روال تا رسيدن به نقاطي که ديگر تغيير نميکنند، ادامه پيدا کرده است.  a  b  c  d  e  f شکل 11: مثالي براي روش خوشهبندي K-Means مشکلات روش خوشهبندي K-Means عليرغم اينکه خاتمهپذيري الگوريتم بالا تضمين شده است ولي جواب نهايي آن واحد نبوده و همواره جوابي بهينه نميباشد. به طور کلي روش ساده بالا داراي مشکلات زير است. * جواب نهايي به انتخاب خوشههاي اوليه وابستگي دارد. * روالي مشخص براي محاسبة اولية مراکز خوشهها وجود ندارد. * اگر در تکراري از الگوريتم تعداد دادههاي متعلق به خوشهاي صفر شد راهي براي تغيير و بهبود ادامة روش وجود ندارد. * در اين روش فرض شده است که تعداد خوشهها از ابتدا مشخص است. اما معمولا در کاربردهاي زيادي تعداد خوشهها مشخص نميباشد. الگوريتم خوشهبندي LBG همانگونه که ذکر شد الگوريتم خوشهبندي K-Means به انتخاب اولية خوشهها بستگي دارد و اين باعث ميشود که نتايج خوشهبندي در تکرارهاي مختلف از الگوريتم متفاوت شود که اين در بسياري از کاربردها قابل نيست. براي رفع اين مشکل الگوريتم خوشهبندي LBG پيشنهاد شد که قادر است به مقدار قابل قبولي بر اين مشکل غلبه کند.[7] در اين روش ابتدا الگوريتم تمام دادهها را به صورت يک خوشه در نظر ميگيرد و سپس براي اين خوشه يک بردار مرکز محاسبه ميکند.(اجراي الگوريتم K-Means با تعداد خوشة 1K=). سپس اين بردار را به 2 بردار ميشکند و دادهها را با توجه به اين دو بردار خوشهبندي ميکند (اجراي الگوريتم K-Means با تعداد خوشة K=2 که مراکز اوليه خوشهها همان دو بردار هستند). در مرحلة بعد اين دو نقطه به چهار نقطه شکسته ميشوند و الگوريتم ادامه پيدا ميکند تا تعداد خوشة مورد نظر توليد شوند. الگوريتم زير را ميتوان براي اين روش خوشهبندي در نظر گرفت: 1. شروع: مقدار M(تعداد خوشهها) با عدد 1 مقدار دهي اوليه ميشود. سپس براي تمام دادهها بردار مرکز محاسبه ميشود. 2. شکست: هر يک از M بردار مرکز به 2 بردار جديد شکسته ميشوند تا 2M بردار مرکز توليد شود. هر بردار جديد بايستي درون همان خوشه قرار داشته باشد و به اندازة کافي از هم دور باشند. 3. K-Means: با اجراي الگوريتم K-Means با تعداد خوشة 2M و مراکز اوليه خوشههاي محاسبه شده در مرحلة ii خوشههاي جديدي با مراکز جديد توليد ميشود. 4. شرط خاتمه: در صورتي که M برابر تعداد خوشة مورد نظر الگوريتم LBG بود الگوريتم خاتمه مييابد و در غير اين صورت به مرحلة ii رفته و الگوريتم تکرار ميشود. |
|
|

|
| #ADS | |
|
نشان دهنده تبلیغات
تبليغگر
تاريخ عضويت: -
محل سكونت: -
سن: 2010
پست ها: -
|
|
|
|
|
|
#12 (لینک دائم) |
|
Administrator
 |
خوشهبندي بر اساس چگالي
اين روشهاي خوشهبندي بر اين اصل استوارند که خوشهها، ناحيههايي از فضاي داده با چگالي زيادي هستند که توسط نواحي با چگالي کمتر از همديگر جدا شدهاند. براي پيادهسازي اين روشهاي خوشهبندي لازم است تا ابتدا اصطلاحاتي تعريف شوند: چگالي نقاط محلي در نقطة P (Local Point Density) : اگر P را نقطة هستة يک همسايگي و ε شعاع همسايگي براي نقطة P در نظر گرفته شود آنگاه همسايگي به شعاع ε براي نقطة P به صورت زير تعريف ميشود:  به تعداد نقاط قرار گرفته شده درون يک همسايگيِ داده شده چگالي نقاط آن همسايگي گفته ميشود.  شکل 12: يک همسايگي براي P داراي چگالي نقاط 5 در دسترسِ مستقيمِ چگالي (Directly Density-Reachable): دادة p را در دسترسِ مستقيمِ چگاليِ q گويند اگر p درون يک همسايگي به شعاع ε با هستة q باشد. در شکل زير بهتر ميتوان اين مفهوم را درک کرد.  شکل 13: p در دسترسِ مستقيمِ چگاليِ q قرار دارد. در دسترسِ چگالي (Density-Reachable): دادة p را در دسترسِ چگاليِ q گويند اگر دادهاي وجود داشته باشد که هم درون يک همسايگي به شعاع ε با هستة p و هم درون يک همسايگي به شعاع ε با هستة q باشد. در شکل زير بهتر ميتوان اين مفهوم را درک کرد  شکل 14: p در دسترسِ چگاليِ q قرار دارد. متصلِ چگالي (Density-Connected): دادة p را متصلِ چگاليِ q گويند اگر دادهاي مانند o وجود داشته باشد که هم در دسترسِ چگاليِ p و هم در دسترسِ چگاليِ q باشد. در شکل زير بهتر ميتوان اين مفهوم را درک کرد.  شکل 15: p متصلِ چگاليِ q است خوشة مبتني بر چگالي (Density-Based Cluster): زير مجموعهاي غيرتهي(S) از مجموعة دادهها (D) که داراي دو شرط زير باشد: § حداکثر: اگر p درون S باشد و q در دسترسِ چگاليِ p باشد آنگاه q نيز متعلق به S باشد. § اتصال: هر دادة درون S متصلِ چگاليِ ساير دادههاي درون S باشد. o خوشهبندي بر اساس چگالي (Density-Based Clustering): خوشهبندي بر اساس چگالي بر روي مجموعة دادة D مجموعهاي به صورت {S1, …, Sn, N} است که : § S1, …, Sn تمام خوشههاي مبتني چگاليِ درون D است. § N=D\{ S1, …, Sn } مجموعة نويز خوانده ميشود.  شکل 16: خوشهبندي بر اساس چگالي الگوريتم خوشهبندي براساس چگالي DBSCAN: در اين روش خوشهبندي هر دادة متعلق به خوشة C در دسترس چگالي ساير دادههاي متعلق به آن خوشه است و در دسترس چگالي هيچ دادة ديگري قرار ندارد. شبه کد اين الگوريتم را زير مشاهده ميکنيد.  1-1-1- مثالي از الگوريتم خوشهبندي براساس چگالي DBSCAN: در شکل زير سعي شده است تا نحوة اعمال الگوريتم خوشهبندي DBSCAN را بر روي يک مجموعه داده نشان داده شود. همانگونه که مشاهده ميشود، اين الگوريتم نوانسته است به خوبي دادهها را خوشهبندي کند. a  b  c:  d:  f :  شکل 17: مثالي از روش خوشهبندي DBSCAN الگوريتم سلسله مراتبي خوشهبندي براساس چگالي OPTICS: در اين روش سعي ميشود تا با تکنيکي سلسله مراتبي خوشههاي بزرگتري را از ترکيب خوشهاي داراي چگالي زياد ولي کوچکتر محاسبه کرد. در شکل زير با يک بار اعمال الگوريتم خوشهبندي DBSCAN خوشههاي C1 و C2 حاصل گشتهاند که در مرحلة ديگري با هم ترکيب شده و خوشة بزرگتر C را ساختهاند. در اين روش با افزايش تعداد تکرار مقدار پارامتر ε افزايش مييابد.  شکل 18: در روش سلسله مراتبي خوشهبندي براساس چگالي OPTICS از ترکيب خوشههاي با چگالي زياد و کوچک خوشههاي بزرگتري حاصل ميشود. مزاياي خوشهبندي بر اساس چگالي a. خوشهها ميتوانند داراي اشکال دلخواه باشند. b. تعداد خوشهها به صورت اتوماتيک همزمان با عمل خوشهبندي تعيين ميشود. c. در تشخيص نويزها بسيار کارا هستند. |
|
|

|
| از Astaraki تشكر كرده اند: | dr_bijan (۰۹-۲۵-۱۳۹۲), shadi.mahmoudi (۰۵-۳-۱۳۹۱) |
|
|
#13 (لینک دائم) |
|
Administrator
 |
بررسي تکنيکهاي اندازهگيري اعتبار خوشهها
نتايج حاصل از اعمال الگوريتمهاي خوشهبندي روي يک مجموعه داده با توجه به انتخابهاي پارامترهاي الگوريتمها ميتواند بسيار متفاوت از يکديگر باشد. هدف از اعتبارسنجي خوشهها يافتن خوشههايي است که بهترين تناسب را با دادههاي مورد نظر داشته باشند. دو معيارِ پاية اندازهگيري پيشنهاد شده براي ارزيابي و انتخاب خوشههاي بهينه عبارتند از:[8] * تراکم (Compactness): دادههاي متعلق به يک خوشه بايستي تا حد ممکن به يکديگر نزديک باشند. معيار رايج براي تعيين ميزان تراکم دادهها واريانس دادهها است. * جدايي (Separation): خوشهها خود بايستي به اندازه کافي از يکديگر جدا باشند. سه راه براي سنجش ميزان جدايي خوشهها مورد استفاده قرار ميگيرد که عبارتند از: * فاصلة بين نزديکترين دادهها از دو خوشه * فاصلة بين دورترين دادهها از دو خوشه * فاصلة بين مراکزخوشهها همچنين روشهاي ارزيابي خوشههاي حاصل از خوشهبندي را به صورت سه دسته تقسيم ميکنند که عبارتند از: * معيارهاي خروجي (External Criteria) * معيارهاي دروني (Internal Criteria) * معيارهاي نسبي (Relative Criteria) هم معيارهاي خروجي و هم معيارهاي دروني بر مبناي روشهاي آماري عمل ميکنند و پيچيدگي محاسباتي بالايي را نيز دارا هستند. معيارهاي خروجي عمل ارزيابي خوشهها را با استفاده از بينش خاص کاربران انجام ميدهند. معيارهاي دروني عمل ارزيابي خوشهها را با استفاده از مقاديري که از خوشهها و نماي آنها محاسبه ميشود، انجام ميدهند. پايه معيارهاي نسبي، مقايسة بين شماهاي خوشهبندي (الگوريم به علاوة پارامترهاي آن) مختلف است. يک و يا چندين روش مختلف خوشهبندي چندين بار با پارامترهاي مختلف روي يک مجموعة داده اجرا ميشوند و بهترين شماي خوشهبندي از بين تمام شماها انتخاب ميشود. در اين روش مبناي مقايسه، شاخصهاي اعتبارسنجي (Validity-Index) هستند. شاخصهاي ارزيابي بسيار متنوعي پيشنهاد شدهاند که در اين قسمت سعي ميشوند تعدادي از رايجترين آنها معرفي شوند. شاخصهاي اعتبارسنجي شاخصهاي اعتبارسنجي براي سنجش ميزان صحت (Goodness) نتايج خوشهبندي به منظور مقايسة بين روشهاي خوشهبندي مختلف يا مقايسة نتايج حاصل از يک روش با پارامترهاي مختلف مورد استفاده قرار ميگيرند. در جدول زير مجموعهاي از علائم استفاده شده در ادامة اين بخش ارائه شده است: 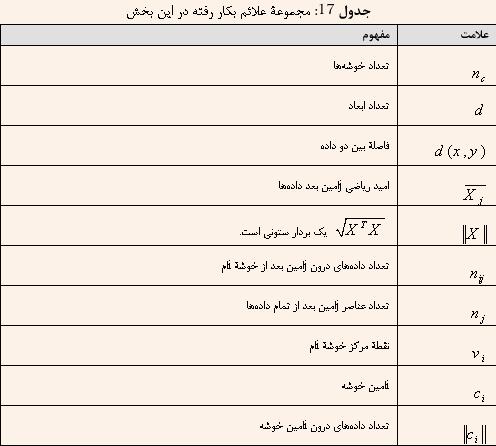 1-1-1- شاخص دون (Dunn Index) اين معيار توسط رابطة زير تعريف ميشود:  که d(x,y) و diam(ci) در آن به ترتيب با روابط 9 و 10 محاسبه ميشوند.   اگر مجموعة دادهاي، داراي خوشههايي جداپذير باشد، انتظار ميرود فاصلة بين خوشهها زياد و قطر خوشههاي (Diameter) آن کوچک باشد. در نتيجه مقداري بزرگتر براي رابطة اين معيار مقداري مطلوبتر است. معايب اين معيار عبارتند از: * محاسبة زمانبر * حساسيت به نويز (قطر خوشهها در صورت وجود يک دادة نويزي ميتواند بسيار تغيير کند.) 1-1-2- شاخص ديويس بولدين (Davies Bouldin Index) اين معيار از شباهت بين دو خوشه (Rij) استفاده ميکند که بر اساس پراکندگي يک خوشه (si) و عدم شباهت بين دو خوشه (dij) تعريف ميشود. شباهت بين دو خوشه را ميتوان به صورتهاي مختلفي تعريف کرد ولي بايستي شرايط زير را دارا باشد. *  *  * اگر si و sj هر دو برابر صفر باشند آنگاه Rij نيز برابر صفر باشد. * اگر  و و  آنگاه آنگاه  * اگر  و و  آنگاه آنگاه  معمولا شباهت بين دو خوشه به صورت زير تعريف ميشود:  که در آن dij و si با روابط زير محاسبه ميشوند.   با توجه به مطالب بيان شده و تعريف شباهت بين دو خوشه شاخص ديويس بولدين به صورت زير تعريف ميشود.  که Ri در آن به صورت زير محاسبه ميشود.  اين شاخص در واقع ميانگين شباهت بين هر خوشه با شبيهترين خوشة به آن را محاسبه ميکند. ميتوان دريافت که هرچه مقدار اين شاخص بيشتر باشد، خوشههاي بهتري توليد شده است. 1-1-3- شاخصهاي اعتبارسنجي ريشة ميانگين مربع انحراف از معيار (RMSSDT) و ريشة R (RS): هرچند اين شاخصها معمولا در اعتبارسنجي الگوريتمهاي سلسله مراتبي مورد استفاده قرار ميگيرند ولي قابليت ارزيابي نتايج ساير تکنيکهاي خوشهبندي را نيز دارا ميباشند. در شاخص اعتبارسنجي RMSSDT (root – mean– square standard deviation) از واريانس خوشهها استفاده ميشود که به شکل رسمي ميتوان از رابطة 16 براي محاسبه آن استفاده کرد.  با توجه به رابطة بالا و اينکه اين معيار ميزان همگني خوشهها را اندازه ميگيرد، ميتوان دريافت که هرچه مقدار آن کمتر باشد نشان دهندة خوشهبندي بهتر دادهها است. شاخص اعتبارسنجي RS (R Square) که با استفاده از رابطة 17، 18 و 19 تعريف ميشود، معياري براي بيان عدمتشابه بين خوشهها است. به اين شاخص درجة همگني بين گروهي نيز گفته ميشود. مقادير آن به بازة اعداد بين 0 تا 1 محدود ميباشد. که 0 نشان دهندة نبودن هيچ تفاوتي بين خوشهها و 1 نشان دهندة وجود تفاوتي قابل توجه بين خوشهها است.    1-1-4- شاخص اعتبارسنجي sd اساس شاخص اعتبارسنجي SD، مياگين پراکندگي (Avrage Scattering) و جدايي کلي (Total Sepration) خوشهها است. پراکندگي از طريق محاسبة واريانس خوشهها و واريانس کل محموعة دادهها بدست ميآيد. با توجه به اينکه اين معيار هم از ميزان همگني دادهها و هم از ميزان تراکم خوشهها بهره ميبرد معيار مناسبي براي ارزيابي خوشهها محسوب ميشود. واريانس مجموعة دادهها را با روابط 20 و 21 و نيز واريانس يک خوشه را با روابط 22 و 23 ميتوان محاسبه کرد. واريانس مجموعه داده ها:   واريانس يک خوشه:   با توجه به واريانسهاي محاسبه شده با روابط بالا، ميانگين پراکندگي خوشهها از رابطة زير محاسبه ميشود.  همچنين ميزان جدايي کلي دادهها که بر اساس فاصلة مراکز خوشهها از هم تعريف ميشود، از رابطة زير محاسبه ميشود.  در نهايت شاخص SD با رابطة زير تعريف ميشود.  که α عمل وزني براي رابطه است که برابر ميزان جدايي خوشهها در صورت داشتن حداکثر تعداد خوشهها ميباشد. مقدار محاسبه شده توسط اين معيار هرچه کوچکتر باشد به معني خوشهبندي بهتر است. 1-1-5- شاخص اعتبارسنجي S_Dbw همانند شاخص SD اين معيار هم بر اساس تراکم درونخوشهاي و ميزان جدايي خوشهها اما در اين شاخص سعي شده تا چگالي خوشهها نيز دخيل شود. به شکل رسمي ميتوان گفت که شاخص S_Dbw از واريانس بين خوشهاي و واريانس درون خوشهاي استفاده ميکند. واريانس بين خوشهها مقدار ميانگين پراکندگي خوشهها را بدست ميآورد که در رابطة 24 نحوة محاسبة آن بيان شده است. مقدار چگالي درون خوشهاي نيز با رابطة زير محاسبه ميشود.  که uij که در آن نقطة وسط خطي است که vi و vj را به هم وصل ميکند. براي محاسبة تابع چگالي اطراف يک نقطه، تعداد نقاط درون ابر کرهاي را که شعاع آن برابر ميانگين انحراف از معيار خوشهها است، شمارش ميشود. ميانگين انحراف از معير خوشهها به صورت زير تعريف ميشود.  در نهايت معيار S_Dbw به صورت زير تعريف ميشود.  در شاخص S_Dbw سعي شده هر دو معيار خوبي خوشهها با هم ترکيب شوند و تخميني دقيق از خوشههاي خاصل بدست آيد. مقدار کم براي اين شاخص به معني خوشهبندي بهتر است. |
|
|

|
| از Astaraki تشكر كرده است: | dr_bijan (۰۹-۲۵-۱۳۹۲) |
|
|
#14 (لینک دائم) |
|
Administrator
 |
1-2- آزمايش ومقايسه کارايي شاخصهاي اعتبار سنجي
در اينجا با آزمايش سعي ميشود کارايي 4 شاخص از شاخصهاي خوشهبندي بالا با هم مقايسه شوند. براي اين منطور از سه دسته داده با ويژگيهاي متفاوت استفاده ميشود. º خوشههاي کاملا جدا: دادههاي متعلق به هر خوشه در کاملا به هم نزديک هستند. شکل 19.a º خوشههاي حلقهاي شکل: خوشهاي که خوشهاي ديگر درون آن قرار دارد. شکل 19.b º خوشههاي با شکل دلخواه: دو خوشه با شکلي دلخواه. شکل 19.c  a  b  c شکل 19: مجموعه دادههاي بکار رفته براي مقايسة کارايي شاخصهاي اعتبارسنجي خوشهها در آزمايش اول از الگوريتم K-Means استفاده شده به گونهاي که يک بار نتيجه درست و بار ديکر نتيجة نادرستي از آن حاصل شده است. سپس نتايج با 4 شاخص دون، ديويس بلودين، SD و D_Dbw اعتبارسنجي شدهاند که در مقادير مربوطه در شکل 20 نشان داده شدهاند  شکل20: مقادير مربوط به شاخصهاي اعتبار بر روي نتايج حاصل از خوشهبندي دادهها کاملا مجزا در آزمايش دوم نتايج حاصل از خوشهبندي مجموعه دادههاي حلقوي شکل که يک بار با روش K-Means به صورت نادرستي خوشهبندي شدهاند و بار ديگر با روش DBSCAN به درستي خوشهبندي شدهاند، با هم مقايسه شدهاند. مقادير محاسبه شده براي شاخصها در شکل 21 نشان داده شده است.  شکل 21: مقادير مربوط به شاخصهاي اعتبار بر روي نتايج حاصل از خوشهبندي دادهها حلقوي نتايج نشان ميدهند که شاخص دون و S_Dbw مقادير صحيحي ولي دو شاخص ديگر مقادير اشتباهي را بدست آوردهند. در آزمايش آخر دادههاي با شکل دلخواه به صورتي که در شکل 22 مشاهده ميشوند خوشهبندي شدهاند که مقادير حاصل از شاخصها بر روي آنها در شکل 23 مشاهده ميشود.  شکل 22: دو حالت خوشهبندي درست و نادرست دادههاي با شکل دلخواه  شکل 23: مقادير مربوط به شاخصهاي اعتبار بر روي نتايج حاصل از خوشهبندي دادهها با شکل دلخواه نتايج اين آزمايش نشان ميدهد که تنها شاخص دون مقادير صحيحي را محاسبه کرده است. |
|
|

|
| از Astaraki تشكر كرده اند: |
|
|
#15 (لینک دائم) |
|
Administrator
 |
خلاصه و نتيجهگيري
خوشهبندي همانگونه که بيان شد، به کشف گروههايي از دادههاي مشابه درون مجموعهاي از دادهها ميپردازد، بدون هيچ اطلاع قبلي از کلاسهاي مربوط به دادهها. انواعي از روشهاي خوشهبندي تاکنون ارائه شدهاندکه وابسته به کاربرد ميتوان از آنها استفاده کرد. در ادامه گروهي از اين روشهاي که به الگوريتمهاي سلسله مراتبي خوشهبندي معروف هستند و يک نمودار که اولويت ترکيب دادهها براي توليد خوشهها را ارائه ميدهد، بررسي شد. سپس روش خوشهبندي K-Means که روشي پايهاي براي بسياري از روشهاي خوشهبندي جديد محسوب ميشود، معرفي شد. پس از آن چند تکنيک خوشهبندي ديگر که از چگالي دادهها براي خوشهبندي استفاده ميکنند، ارائه شدند که اين روش براي خوشهبندي دادههاي با اشکال دلخواه بسيار بهتر از ساير روشها عمل ميکنند. در ادامه تکنيکهايي براي ارزيابي و سنجش خوشههاي حاصل از خوشهبندي ارائه شده که از طريق آنها ميتوان پارامترهاي هر يک از روشهاي مذکور را به صورتي که نتيجة بهتري حاصل شود تعيين کرد. با توجه به کاربرد روزافزون خوشهبندي، امروزه شاهد ارائة روشهاي جديد و کاراتري هستيم که هر يک براي کاربردي خاص ارائه ميشود. همچين شاخصهاي اعتبارسنجي زيادي نيز براي بهترکردن نتيجة خوشهبندي معرفي ميشوند ولي با همة اين تلاشها هنوز خوشهبندي در بسياري از علوم آنچنان که بايد بکار گرفته شود، مورد استفاده قرار نگرفته است قابليت گسترش بسيار زيادي براي آن وجود دارد. در فايل pdf زير همه ي مطالب جمع آوري شده  
__________________
       ويرايش شده توسط Astaraki; ۰۶-۱۴-۱۳۸۹ در ساعت ۰۳:۲۴ بعد از ظهر |
|
|

|
| از Astaraki تشكر كرده اند: | dare (۰۴-۲۸-۱۳۹۰), diamond222170 (۰۳-۱۶-۱۳۹۴), dr_bijan (۰۹-۲۵-۱۳۹۲), engineer_yasin (۰۴-۲۹-۱۳۸۹), farshad1362 (۰۹-۱۰-۱۳۹۰), hamid_akbari (۰۱-۲۰-۱۳۹۱), hannane (۱۰-۲۴-۱۳۹۰), ITman2010 (۰۳-۲۱-۱۳۹۱), it_heidari (۰۳-۳-۱۳۹۳), manchester_love (۰۷-۱۱-۱۳۸۹), msrostami (۰۳-۹-۱۳۸۹), negar_a (۱۲-۶-۱۳۸۹), rezanasiripour (۰۴-۱۸-۱۳۹۲), shadi.mahmoudi (۰۵-۳-۱۳۹۱), |مریم (۱۱-۲۲-۱۳۹۲) |
|
|
#16 (لینک دائم) |
|
عضو جدید
 |
برنامه اینا رو کسی نوشته؟ یعنی کد ساده ای در این مورد وجود داره؟
|
|
|

|
| از hamidrezas تشكر كرده اند: | farshad1362 (۰۹-۱۰-۱۳۹۰), galva (۰۲-۲۵-۱۳۹۰) |
|
|
#17 (لینک دائم) |
|
عضو جدید
 تاريخ عضويت: اسفند ۱۳۸۸
پست ها: 1
تشكرها: 0
1 تشكر در 1 پست
|
اگه بلدید لطفا راهنمایی کنید
|
|
|

|
| از rudbari تشكر كرده است: | farshad1362 (۰۹-۱۰-۱۳۹۰) |
|
|
#18 (لینک دائم) | |
|
عضو جدید
 تاريخ عضويت: خرداد ۱۳۹۶
پست ها: 2
تشكرها: 0
0 تشكر در 0 پست
|
نقل قول:
|
|
|
|

|
|
|
#19 (لینک دائم) |
|
عضو جدید
 تاريخ عضويت: خرداد ۱۳۹۶
پست ها: 2
تشكرها: 0
0 تشكر در 0 پست
|
با سلام و وقت بخیر ممنون میشم منبع و درصورت بودن مقالاتی که این متن از آن برداشت شده اند بفرمایید،خیلی ضروریه برام ،با تشکر فراوان
http://artificial.ir/intelligence/thread1464.html مقدمهاي بر خوشهبندي خوشهبندي را ميتوان به عنوان مهمترين مسئله در يادگيري بدون نظارت در نظر گرفت. خوشهبندي با يافتن يک ساختار درون يک مجموعه از دادههاي بدون برچسب درگير است. خوشه به مجموعهاي از دادهها گفته ميشود که به هم شباهت داشته باشند. در خوشهبندي سعي ميشود تا دادهها به خوشههايي تقسيم شوند که شباهت بين دادههاي درون هر خوشه حداکثر و شباهت بين دادههاي درون خوشههاي متفاوت حداقل شود. شکل 1: در اين شکل نمونهاي از اعمال خوشهبندي روي يک مجموعه از دادهها مشخص شده است که از معيار فاصله(Distance) به عنوان عدم شباهت(Dissimilarity) بين دادهها استفاده شده است. خوشهبندي در مقابل طبقهبندي در طبقهبندي هر داده به يک طبقه (کلاس) از پيشين مشخص شده تخصيص مييابد ولي در خوشهبندي هيچ اطلاعي از کلاسهاي موجود درون دادهها وجود ندارد و به عبارتي خود خوشهها نيز از دادهها استخراج ميشوند. در شکل زير تفاوت بين خوشهبندي و طبقهبندي بهتر نشان داده شده است. ایرانی2017 آنلاين است ارجاع دادن پيام |
|
|

|
 |
| كاربران در حال ديدن تاپيک: 1 (0 عضو و 1 مهمان) | |
|
|
زمان محلي شما با تنظيم GMT +3.5 هم اکنون ۰۹:۱۰ بعد از ظهر ميباشد.











 Linear Mode
Linear Mode







