 |
Ш§ЩҶШ¬Щ…ЩҶ ШұШ§ ШҜШұ ЪҜЩҲЪҜЩ„ Щ…ШӯШЁЩҲШЁ Ъ©ЩҶЩҠШҜ :
|
|||||||
| Ш«ШЁШӘ ЩҶШ§Щ… | Ш§ШұШіШ§Щ„ ШҜШ№ЩҲШӘЩҶШ§Щ…ЩҮ ШЁЩҮ ШҜЩҲШіШӘШ§ЩҶ ! | ШұШ§ЩҮЩҶЩ…Ш§ЩҠ ШіШ§ЩҠШӘ | Community | ШӘЩӮЩҲЩҠЩ… | Ш§ШұШіШ§Щ„ЩҮШ§ЩҠ Ш§Щ…ШұЩҲШІ | Ш¬ШіШӘШ¬ЩҲ |
 |
| ШӘШЁЩ„ЩҠШәШ§ШӘ ШіШ§ЩҠШӘ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  |
|
|
|
LinkBack | Ш§ШЁШІШ§ШұЩҮШ§ЩҠ ШӘШ§ЩҫЩҠЪ© | ЩҶШӯЩҲЩҮ ЩҶЩ…Ш§ЩҠШҙ |
|
|
|
|
#1 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Щ…ШіШҰЩ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮвҖҢЪҜШұШҜ (ШЁЩҮ Ш§ЩҶЪҜЩ„ЫҢШіЫҢ: Travelling salesman problem ШҢ ШЁЩҮвҖҢШ§Ш®ШӘШөШ§Шұ: TSP )
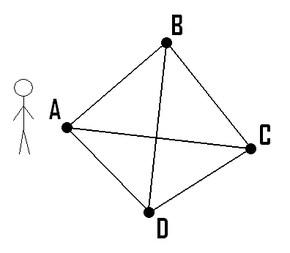 Ш§ЪҜШұ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮвҖҢЪҜШұШҜ Ш§ШІ ЩҶЩӮШ·ЩҮ A ШҙШұЩҲШ№ Ъ©ЩҶШҜ ЩҲ ЩҒЩҲШ§ШөЩ„ ШЁЫҢЩҶ ЩҶЩӮШ§Ш· Щ…ШҙШ®Шө ШЁШ§ШҙШҜШҢ Ъ©ЩҲШӘШ§ЩҮвҖҢШӘШұШЁЩҶ Щ…ШіЫҢШұ Ъ©ЩҮ Ш§ШІ ШӘЩ…Ш§Щ… ЩҶЩӮШ§Ш· ЫҢЪ©ШЁШ§Шұ ШЁШ§ШІШҜЫҢШҜ Щ…ЫҢвҖҢЪ©ЩҶШҜ ЩҲ ШЁЩҮ A ШЁШ§ШІЩ…ЫҢвҖҢЪҜШұШҜШҜ Ъ©ШҜШ§Щ… Ш§ШіШӘШҹ ........ Щ…ШіШҰЩ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮ ЪҜШұШҜ TSP ЫҢЪ©ЫҢ Ш§ШІ Щ…ШіШ§ШҰЩ„ Щ…ЩҮЩ… ШҜШұ ШІЩ…ШұЩҮ ШӘШҰЩҲШұЫҢ ЩҫЫҢЪҶЫҢШҜЪҜЫҢ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ЩҮШ§ Щ…ЫҢ ШЁШ§ШҙШҜ Ъ©ЩҮ ШҜШұ ЪҜШұЩҲЩҮ NP-Hard ЩӮШұШ§Шұ Щ…ЫҢ ЪҜЫҢШұШҜ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ Ш§ЩҲЩ„ЫҢЩҶ ШЁШ§Шұ ШӘЩҲШіШ· ШҜЩҲ ШҜШ§ЩҶШҙЩ…ЩҶШҜ ШЁЩҮ ЩҶШ§Щ… ЩҮШ§ЫҢ 1- ЩҮШ§Щ…ЫҢЩ„ШӘЩҲЩҶ Ш§ЫҢШұЩ„ЩҶШҜЫҢ ЩҲ 2- Ъ©ЫҢШұЪ©Щ…ЩҶ ШЁШұЫҢШӘШ§ЩҶЫҢШ§ЫҢЫҢ Щ…Ш·ШұШӯ ШҙШҜ . Щ…Ш№Щ…ЩҲЩ„Ш§ ШЁШӯШ« ШҜШұ Ш®ШөЩҲШө Ш§ЫҢЩҶ ШӘШҰЩҲШұЫҢ ШҜШұ Щ…Ш·Ш§Щ„ШЁ Ш§ЩҲЩ„ЫҢЩҮ ШҜШұЩҲШі ШұЫҢШ§Ш¶ЫҢШ§ШӘ ШҜШ§ЩҶШҙШ¬ЩҲЫҢШ§ЩҶ ШұЫҢШ§Ш¶ЫҢ Ш§ШұШ§ШҰЩҮ Щ…ЫҢ ШҙЩҲШҜ ЩҲ ШҜШұ ШҜШұЩҲШіЫҢ ЩҶШёЫҢШұ ШӘШҰЩҲШұЫҢ ЪҜШұШ§ЩҒ Щ…ЫҢ ШӘЩҲШ§ЩҶЫҢШҜ Щ…Ш·Ш§Щ„ШЁ Щ…ШҙШ§ШЁЩҮ ШұШ§ ЩҶЫҢШІ ШЁШҜШіШӘ ШўЩҲШұЫҢШҜ . Ш·ШұШӯ Щ…ШіШҰЩ„ЩҮ ШӘШ№ШҜШ§ШҜЫҢ ШҙЩҮШұ ШҜШ§ШұЫҢЩ… ЩҲ ЩҮШІЫҢЩҶЩҮ (Щ…ШіШ§ЩҒШӘ) Щ…ШіШ§ЩҒШұШӘ ШЁЩҮ ЩҮШұ ЫҢЪ© Ш§ШІ ШўЩҶЩҮШ§ Щ…ШҙШ®Шө Ш§ШіШӘ ШЁЩҮ ШҜЩҶШЁШ§Щ„ Ъ©Щ… ЩҮШІЫҢЩҶЩҮ ШӘШұЫҢЩҶ Щ…ШіЫҢШұ ЩҮШіШӘЫҢЩ… ШЁШ·ЩҲШұЫҢЪ©ЩҮ Ш§ШІ ЩҮЩ…ЩҮ ШҙЩҮШұЩҮШ§ ЩҒЩӮШ· ЫҢЪ©ШЁШ§Шұ Ш№ЫҢЩҲШұ Ъ©ЩҶЫҢЩ… ЩҲ Щ…Ш¬ШҜШҜШ§ ШЁЩҮ Щ…ШӯЩ„ ШҙШұЩҲШ№ ШЁШ§ШІЪҜШұШҜЫҢЩ… ЩҫЫҢЪҶЫҢШҜЪҜЫҢ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮ ЪҜШұШҜ Ш§ЫҢЩҶ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ШЁШ·ЩҲШұ Щ…ШіШӘЩӮЫҢЩ… ШҜШұ Щ…ШұШӘШЁЩҮ ШІЩ…Ш§ЩҶЫҢ(!O(n ШӯЩ„ Щ…ЫҢ ШҙЩҲШҜ Ш§Щ…Ш§ Ш§ЪҜШұ ШЁЩҮ ШұЩҲШҙ ШЁШұЩҶШ§Щ…ЩҮ ЩҶЩҲЫҢШіЫҢ ЩҫЩҲЫҢШ§ ШЁШұШ§ЫҢ ШӯЩ„ ШўЩҶ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ЩҶЫҢЩ… Щ…ШұШӘШЁЩҮ ШІЩ…Ш§ЩҶЫҢ ШўЩҶ (O(n^2*2^n Ш®ЩҲШ§ЩҮШҜ ШҙШҜ Ъ©ЩҮ Ш¬ШІ Щ…ШұШӘШЁЩҮ ЩҮШ§ЫҢ ЩҶЩ…Ш§ЫҢЫҢ Ш§ШіШӘ. ШЁШ§ЫҢШҜ ШӘЩҲШ¬ЩҮ ШҜШ§ШҙШӘ Ш№Щ„ЫҢ ШұШәЩ… ШўЩҶЪ©ЩҮ Щ…ШұШӘШЁЩҮ ЩҶЩ…Ш§ЫҢЫҢ Щ…Ш°Ъ©ЩҲШұ ШІЩ…Ш§ЩҶ ШЁШіЫҢШ§Шұ ШЁШҜЫҢ Ш§ШіШӘ Ш§Щ…Ш§ ЩҮЩ…ЪҶЩҶШ§ЩҶ ШЁШіЫҢШ§Шұ ШЁЩҮШӘШұ Ш§ШІ Щ…ШұШӘШЁЩҮ ЩҒШ§Ъ©ШӘЩҲШұЫҢЩ„ Щ…ЫҢ ШЁШ§ШҙШҜ . .............. ШҙШЁЩҮ Ъ©ШҜ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ЩҒЩҲЩӮ ШЁШөЩҲШұШӘ ШІЫҢШұ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШўЩҶ ШӘШ№ШҜШ§ШҜ ШІЫҢШұ Щ…Ш¬Щ…ЩҲШ№ЩҮ ЩҮШ§ЫҢ ЫҢЪ© Щ…Ш¬Щ…ЩҲШ№ЩҮ n Ш№Ш¶ЩҲЫҢ 2 ШЁЩҮ ШӘЩҲШ§ЩҶ n Щ…ЫҢ ШЁШ§ШҙШҜ ЩҲ for Ш§ЩҲЩ„ ЫҢЪ© Ш¶ШұЫҢШЁ n ШұШ§ ЩҶЫҢШІ ШӯШ§ШөЩ„ Щ…ЫҢ ШҙЩҲШҜ Ъ©ЩҮ ШЁЩҮ Ш§ШІШ§ЫҢ ШӘЩ…Ш§Щ… ШҙЩҮШұЩҮШ§ЫҢ ШәЫҢШұ Щ…ШЁШҜШ§ Щ…ЫҢ ШЁШ§ШҙШҜ ЩҲ ШӯШ§ШөЩ„ (n*(2^n ШұШ§ ЩҫШҜЫҢШҜ Щ…ЫҢ ШўЩҲШұШҜ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШЁШұШ§ЫҢ Ш¬ШіШӘШ¬ЩҲЫҢ Ъ©Щ…ШӘШұЫҢЩҶ Щ…ЩӮШҜШ§Шұ ЩҶЫҢШ§ШІ ШЁЩҮ ЫҢЪ© Ш№Щ…Щ„ЫҢШ§ШӘ Ш®Ш·ЫҢ Ш§ШІ Щ…ШұШӘШЁЩҮ n ШҜШ§ШұЫҢЩ… Ъ©ЩҮ ШҜШұ ШІЩ…Ш§ЩҶ ЩҒЩҲЩӮ ЩҶЫҢШІ Ш¶ШұШЁ Щ…ЫҢ ШҙЩҲШҜ ЩҲ ШҜШұ ЩҶЩҮШ§ЫҢШӘ ШІЩ…Ш§ЩҶ (n^2)*(2^n) ШұШ§ ШЁШұШ§ЫҢ Ш§ЫҢЩҶ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ШӯШ§ШөЩ„ Щ…ЫҢ Ъ©ЩҶШҜ ЩғШҜ:
C({1},1) = 0
for (S=2 to n )
for All Subsets S subset of {1,2,3,...} of size S and containing 1
C(S,1) = &
for All J member of S , J<>1
C ( S , J ) = min { C ( S - { J } , i ) + D i,J : i member of S , i <> J }
return min j C ( {1 . . . n}, J ) + D J,1
Ш§ЩҠЩҶ Щ…ШіШҰЩ„ЩҮ ШҢ Щ…ШіШҰЩ„ЩҮвҖҢШ§ЫҢ Щ…ШҙЩҮЩҲШұ Ш§ШіШӘ Ъ©ЩҮ Ш§ШЁШӘШҜШ§ ШҜШұ ШіШҜЩҮ ЫұЫё Щ…ШіШ§ШҰЩ„ Щ…ШұШЁЩҲШ· ШЁЩҮ ШўЩҶ ШӘЩҲШіШ· ЩҲЫҢЩ„ЫҢШ§Щ… ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶ ЩҲ ШӘЩҲЩ…Ш§Ші Ъ©ШұЪ©Щ…ЩҶ Щ…Ш·ШұШӯ ШҙШҜ ЩҲ ШіЩҫШі ШҜШұ ШҜЩҮЩҮ ЫұЫ№ЫіЫ° ШҙЪ©Щ„ Ш№Щ…ЩҲЩ…ЫҢ ШўЩҶ ШЁЩҮ ЩҲШіЫҢЩ„ЩҮ ШұЫҢШ§Ш¶ЫҢШҜШ§ЩҶШ§ЩҶЫҢ Щ…Ш«Щ„ Ъ©Ш§ШұЩ„ Щ…ЩҶЪҜШұ Ш§ШІ ШҜШ§ЩҶШҙЪҜШ§ЩҮ ЩҮШ§ШұЩҲШ§ШұШҜ ЩҲ ЩҮШ§ШіЩ„Шұ ЩҲЫҢШӘЩҶЫҢ Ш§ШІ ШҜШ§ЩҶШҙЪҜШ§ЩҮ ЩҫШұЫҢЩҶШіШӘЩҲЩҶ Щ…ЩҲШұШҜ Щ…Ш·Ш§Щ„Ш№ЩҮ ЩӮШұШ§Шұ ЪҜШұЩҒШӘ. ШҙШұШӯ Щ…ШіШҰЩ„ЩҮ ШЁШҜЫҢЩҶ ШҙЪ©Щ„ Ш§ШіШӘ: ШӘШ№ШҜШ§ШҜЫҢ ШҙЩҮШұ ШҜШ§ШұЫҢЩ… ЩҲ ЩҮШІЫҢЩҶЩҮ ШұЩҒШӘЩҶ Щ…ШіШӘЩӮЫҢЩ… Ш§ШІ ЫҢЪ©ЫҢ ШЁЩҮ ШҜЫҢЪҜШұЫҢ ШұШ§ Щ…ЫҢвҖҢШҜШ§ЩҶЫҢЩ…. Щ…Ш·Щ„ЩҲШЁ Ш§ШіШӘ Ъ©Щ…вҖҢЩҮШІЫҢЩҶЩҮвҖҢШӘШұЫҢЩҶ Щ…ШіЫҢШұЫҢ Ъ©ЩҮ Ш§ШІ ЫҢЪ© ШҙЩҮШұ ШҙШұЩҲШ№ ШҙЩҲШҜ ЩҲ Ш§ШІ ШӘЩ…Ш§Щ…ЫҢ ШҙЩҮШұЩҮШ§ ШҜЩӮЫҢЩӮШ§ЩҢ ЫҢЪ©ШЁШ§Шұ Ш№ШЁЩҲШұ Ъ©ЩҶШҜ ЩҲ ШЁЩҮ ШҙЩҮШұ ШҙШұЩҲШ№ ШЁШ§ШІЪҜШұШҜШҜ. ШӘШ№ШҜШ§ШҜ Ъ©Щ„ ШұШ§ЩҮвҖҢШӯЩ„вҖҢЩҮШ§ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШЁШұШ§ЫҢ n>ЫІ Ъ©ЩҮ n ШӘШ№ШҜШ§ШҜ ШҙЩҮШұЩҮШ§ Ш§ШіШӘ. ШҜШұ ЩҲШ§ЩӮШ№ Ш§ЫҢЩҶ Ш№ШҜШҜ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШӘШ№ШҜШ§ШҜ ШҜЩҲШұЩҮШ§ЫҢ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ШҜШұ ЫҢЪ© ЪҜШұШ§ЩҒ Ъ©Ш§Щ…Щ„ ШЁШ§ n ШұШЈШі. Щ…ШіШҰЩ„ЩҮвҖҢЩҮШ§ЫҢ Щ…ШұШӘШЁШ· Щ…ШіШҰЩ„ЩҮ Щ…Ш№Ш§ШҜЩ„ ШҜШұ ЩҶШёШұЫҢЩҮ ЪҜШұШ§ЩҒ ШЁЩҮ Ш§ЫҢЩҶ ШөЩҲШұШӘ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ© ЪҜШұШ§ЩҒ ЩҲШІЩҶвҖҢШҜШ§Шұ Ъ©Ш§Щ…Щ„ ШҜШ§ШұЫҢЩ… Ъ©ЩҮ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЫҢЩ… Ъ©Щ…вҖҢЩҲШІЩҶвҖҢШӘШұЫҢЩҶ ШҜЩҲШұ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ШұШ§ ЩҫЫҢШҜШ§ Ъ©ЩҶЫҢЩ…. Щ…ШіШҰЩ„ЩҮ ШӘЩҶЪҜШұШ§ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮвҖҢЪҜШұШҜ (ШЁЩҮ Ш§ЩҶЪҜЩ„ЫҢШіЫҢ: Bottleneck traveling salesman problemШҢ ШЁЩҮвҖҢШ§Ш®ШӘШөШ§Шұ: bottleneck TSP ) Щ…ШіШҰЩ„ЩҮвҖҢШ§ЫҢ ШЁШіЫҢШ§Шұ Ъ©Ш§ШұШЁШұШҜЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ЫҢЪ© ЪҜШұШ§ЩҒ ЩҲШІЩҶвҖҢШҜШ§Шұ Ъ©Щ…вҖҢЩҲШІЩҶвҖҢШӘШұЫҢЩҶ ШҜЩҲШұ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ШұШ§ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮШҜ Ъ©ЩҮ ШҙШ§Щ…Щ„ ШіЩҶЪҜЫҢЩҶвҖҢШӘШұЫҢЩҶ ЫҢШ§Щ„ ШЁШ§ШҙШҜ. ШӘШ№Щ…ЫҢЩ…вҖҢЫҢШ§ЩҒШӘЩҮ Щ…ШіШҰЩ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮвҖҢЪҜШұШҜ ШҜШ§ШұШ§ЫҢ Ш§ЫҢШ§Щ„ШӘвҖҢЩҮШ§ЫҢЫҢ Ш§ШіШӘ Ъ©ЩҮ ЩҮШұ Ъ©ШҜШ§Щ… ШӯШҜШ§ЩӮЩ„ ЫҢЪ© ШҙЩҮШұ ШҜШ§ШұЩҶШҜ ЩҲ ЩҒШұЩҲШҙЩҶШҜЩҮ ШЁШ§ЫҢШҜ Ш§ШІ ЩҮШұ Ш§ЫҢШ§Щ„ШӘ ШҜЩӮЫҢЩӮШ§ЩҢ Ш§ШІ ЫҢЪ© ШҙЩҮШұ Ш№ШЁЩҲШұ Ъ©ЩҶШҜ. Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШЁЩҮ В« Щ…ШіШҰЩ„ЩҮ ШіЫҢШ§ШіШӘвҖҢЩ…ШҜШ§Шұ Щ…ШіШ§ЩҒШұВ» ЩҶЫҢШІ ШҙЩҮШұШӘ ШҜШ§ШұШҜ. Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ Щ…ШіШҰЩ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮвҖҢЪҜШұШҜ Ш¬ШІШЎ Щ…ШіШ§ШҰЩ„ NP-hard Ш§ШіШӘ. ШұШ§ЩҮвҖҢЩҮШ§ЫҢ Щ…Ш№Щ…ЩҲЩ„ Щ…ЩӮШ§ШЁЩ„ЩҮ ШЁШ§ ЪҶЩҶЫҢЩҶ Щ…ШіШ§ШҰЩ„ЫҢ Ш№ШЁШ§ШұШӘЩҶШҜ Ш§ШІ: Ш·ШұШ§ШӯЫҢ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ЫҢЫҢ ШЁШұШ§ЫҢ ЩҫЫҢШҜШ§ Ъ©ШұШҜЩҶ Ш¬ЩҲШ§ШЁвҖҢЩҮШ§ЫҢ ШҜЩӮЫҢЩӮ Ъ©ЩҮ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ШўЩҶЩҮШ§ ЩҒЩӮШ· ШЁШұШ§ЫҢ Щ…ШіШ§ШҰЩ„ ШЁШ§ Ш§ЩҶШҜШ§ШІЩҮ Ъ©ЩҲЪҶЪ© ШөЩҲШұШӘ Щ…ЫҢвҖҢЪҜЫҢШұШҜ. Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ЫҢ Щ…Ъ©Ш§ШҙЩҒЩҮвҖҢШ§ЫҢ Ъ©ЩҮ Ш¬ЩҲШ§ШЁвҖҢЩҮШ§ЫҢЫҢ ШЁЩҮвҖҢШҜШіШӘ Щ…ЫҢвҖҢШҜЩҮШҜ Ъ©ЩҮ Ш§ШӯШӘЩ…Ш§Щ„Ш§ЩҢ ШҜШұШіШӘ ЩҮШіШӘЩҶШҜ. ЩҫЫҢШҜШ§ Ъ©ШұШҜЩҶ ШІЫҢШұЩ…ШіШҰЩ„ЩҮвҖҢЩҮШ§ЫҢЫҢ Ш§ШІ Щ…ШіШҰЩ„ЩҮ ЫҢШ№ЩҶЫҢ ШӘЩӮШіЫҢЩ… Щ…ШіШҰЩ„ЩҮ ШЁЩҮ Щ…ШіШҰЩ„ЩҮвҖҢЩҮШ§ЫҢ Ъ©ЩҲЪҶЪ©ШӘШұ ШӘШ§ ШЁШҙЩҲШҜ Ш§ШІ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ЫҢ Щ…Ъ©Ш§ШҙЩҒЩҮвҖҢШ§ЫҢ ШЁЩҮШӘШұ ЩҲ ШҜЩӮЫҢЩӮвҖҢШӘШұЫҢ Ш§ШұШ§ШҰЩҮ Ъ©ШұШҜ. Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ЫҢ ШҜЩӮЫҢЩӮ ШіШұШұШ§ШіШӘ ШӘШұЫҢЩҶ ШұШ§ЩҮ ШӯЩ„ Ш§Щ…ШӘШӯШ§ЩҶ Ъ©ШұШҜЩҶ ШӘЩ…Ш§Щ…ЫҢ Ш¬Ш§ЫҢЪҜШҙШӘвҖҢЩҮШ§ЫҢ Щ…Щ…Ъ©ЩҶ ШЁШұШ§ЫҢ ЩҫЫҢШҜШ§ Ъ©ШұШҜЩҶ Ш§ШұШІШ§ЩҶвҖҢШӘШұЫҢЩҶ Щ…ШіЫҢШұ Ш§ШіШӘ Ъ©ЩҮ ЪҶЩҲЩҶ ШӘШ№ШҜШ§ШҜ Ш¬Ш§ЫҢЪҜШҙШӘвҖҢЩҮШ§ !n Ш§ШіШӘШҢ Ш§ЫҢЩҶ ШұШ§ЩҮ ШӯЩ„ ШәЫҢШұШ№Щ…Щ„ЫҢ Щ…ЫҢвҖҢШҙЩҲШҜ. ШЁШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ШЁШұЩҶШ§Щ…ЩҮвҖҢЩҶЩҲЫҢШіЫҢ ЩҫЩҲЫҢШ§ Щ…ШіШҰЩ„ЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ШЁШ§ Щ…ШұШӘШЁЩҮ ШІЩ…Ш§ЩҶЫҢ n22n ШӯЩ„ ШҙЩҲШҜ. ШұШ§ЩҮвҖҢЩҮШ§ЫҢ ШҜЫҢЪҜШұ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ЫҢ Ш§ЩҶШҙШ№Ш§ШЁ ЩҲ ШӘШӯШҜЫҢШҜ ШЁШұШ§ЫҢ ЫҙЫ° ШӘШ§ Ы¶Ы° ШҙЩҮШұШҢ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ШЁШұЩҶШ§Щ…ЩҮвҖҢЩҶЩҲЫҢШіЫҢ Ш®Ш·ЫҢ ШЁШұШ§ЫҢ Ъ©ЩҲЪҶЪ©ШӘШұ Ш§ШІ ЫІЫ°Ы° ШҙЩҮШұ ЩҲ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ШұЩҲШҙ ШЁШұШҙ-ШөЩҒШӯЩҮ ШЁШұШ§ЫҢ Ш§ЩҶШҜШ§ШІЩҮвҖҢЩҮШ§ЫҢ ШЁШІШұЪҜ Ш§ШіШӘ. Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ЫҢ Щ…Ъ©Ш§ШҙЩҒЩҮвҖҢШ§ЫҢ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ…вҖҢЩҮШ§ЫҢ ШӘЩӮШұЫҢШЁЫҢ Щ…ШӘЩҶЩҲШ№ЫҢ ЩҲШ¬ЩҲШҜ ШҜШ§ШұЩҶШҜ Ъ©ЩҮ Ш®ЫҢЩ„ЫҢ ШіШұЫҢШ№ Ш¬ЩҲШ§ШЁвҖҢЩҮШ§ЫҢ ШҜШұШіШӘ ШұШ§ ШЁШ§ Ш§ШӯШӘЩ…Ш§Щ„ ШЁШ§Щ„Ш§ ШЁЩҮвҖҢШҜШіШӘ Щ…ЫҢвҖҢШҜЩҮЩҶШҜ Ъ©ЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШўЩҶЩҮШ§ ШұШ§ ШЁЩҮ ШөЩҲШұШӘ ШІЫҢШұ ШҜШіШӘЩҮвҖҢШЁЩҶШҜЫҢ Ъ©ШұШҜ: Щ…Ъ©Ш§ШҙЩҒЩҮвҖҢШ§ЫҢ ШіШ§ШІЩҶШҜЩҮ ШЁЩҮШЁЩҲШҜ ШӘЪ©ШұШ§ШұЫҢ Щ…ШЁШ§ШҜЩ„ЩҮ ШҜЩҲШЁЩҮвҖҢШҜЩҲ Щ…Ъ©Ш§ШҙЩҒЩҮвҖҢШ§ЫҢ k-opt Щ…Ъ©Ш§ШҙЩҒЩҮвҖҢШ§ЫҢ V-opt ШЁЩҮШЁЩҲШҜ ШӘШөШ§ШҜЩҒЫҢ |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | *sepid* (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), ali_85 (Ы°Ыі-ЫІЫ·-ЫұЫіЫ№Ыұ), e-eng (ЫұЫұ-Ы·-ЫұЫіЫёЫ№), elit (Ы°Ы¶-Ы·-ЫұЫіЫ№Ыұ), green_Dream (ЫұЫІ-Ы¶-ЫұЫіЫёЫё), h.jaza (ЫұЫ°-ЫІЫө-ЫұЫіЫёЫё), intell23 (Ы°Ы·-ЫІЫө-ЫұЫіЫ№ЫІ), lesanalgeib (Ы°Ыө-ЫІЫі-ЫұЫіЫ№Ыі), mav (Ы°Ыө-Ыұ-ЫұЫіЫ№ЫІ), minoo007 (Ы°Ыі-ЫұЫ°-ЫұЫіЫ№Ыұ), mitrashooshtari (Ы°ЫІ-ЫІЫ¶-ЫұЫіЫ№Ыұ), nafise 2 (Ы°Ыі-ЫұЫ°-ЫұЫіЫ№Ыұ), r3d.w0rm (Ы°Ы¶-Ыё-ЫұЫіЫ№ЫІ), raika (Ы°Ыө-ЫІЫ°-ЫұЫіЫ№Ыұ), sabora (ЫұЫұ-Ы·-ЫұЫіЫ№Ыұ), saeedeh23 (Ы°Ыі-Ыі-ЫұЫіЫ№Ыұ), samane_89 (Ы°ЫІ-ЫІЫө-ЫұЫіЫ№Ы°), shima mechanic (Ы°ЫІ-ЫұЫі-ЫұЫіЫ№Ыө), snowy_ night (ЫұЫІ-ЫІЫө-ЫұЫіЫёЫё), Solsal (Ы°Ыө-Ыұ-ЫұЫіЫ№Ы°), susaaan (Ы°Ыё-ЫІЫ№-ЫұЫіЫ№Ы°), Щ…ЩҮШіШ§ Ш¬ (Ы°Ыҙ-Ыі-ЫұЫіЫ№Ыҙ), Violet_kia2 (Ы°ЫІ-Ы¶-ЫұЫіЫ№Ы°) |
| #ADS | |
|
ЩҶШҙШ§ЩҶ ШҜЩҮЩҶШҜЩҮ ШӘШЁЩ„ЫҢШәШ§ШӘ
ШӘШЁЩ„ЩҠШәЪҜШұ
ШӘШ§ШұЩҠШ® Ш№Ш¶ЩҲЩҠШӘ: -
Щ…ШӯЩ„ ШіЩғЩҲЩҶШӘ: -
ШіЩҶ: 2010
ЩҫШіШӘ ЩҮШ§: -
|
|
|
|
|
|
#2 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Ш§ШЁШӘШҜШ§ ШіШ§ЩҠШӘЩҮШ§ЩҠЩҠ Ъ©ЩҮ Ъ©ШҜЩҮШ§ЩҠ ШӯЩ„ Ш§ЩҠЩҶ Щ…ШіШҰЩ„ЩҮ ШұШ§ Ш§ШІ ШұЩҲШҙ ЩҮШ§ЩҠ Щ…ШӘЩҒШ§ЩҲШӘ ЩҲ ШІШЁШ§ЩҶЩҮШ§ЩҠ Щ…Ш®ШӘЩ„ЩҒ Ш§ШұШ§ШҰЩҮ Ъ©ШұШҜЩҮ Ш§ЩҶШҜ:
 Source Code Library: Travelling Salesman Problem (TSP Solving Travelling Salesman Problems Using Genetic Algorithms Solution to Travelling Salesman Problem 
|
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | *sepid* (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), ali_85 (Ы°Ыі-ЫІЫ·-ЫұЫіЫ№Ыұ), e-eng (ЫұЫұ-Ы·-ЫұЫіЫёЫ№), h.jaza (ЫұЫ°-ЫІЫө-ЫұЫіЫёЫё), intell23 (Ы°Ы·-ЫІЫө-ЫұЫіЫ№ЫІ), m@r@l (Ы°ЫІ-ЫұЫ°-ЫұЫіЫ№Ыі), mav (Ы°Ыө-Ыұ-ЫұЫіЫ№ЫІ), mitrashooshtari (Ы°ЫІ-ЫІЫ¶-ЫұЫіЫ№Ыұ), saeedeh23 (Ы°Ыі-Ыі-ЫұЫіЫ№Ыұ), snowy_ night (ЫұЫІ-ЫІЫө-ЫұЫіЫёЫё), Solsal (Ы°Ыө-Ыұ-ЫұЫіЫ№Ы°), susaaan (Ы°Ыё-ЫІЫ№-ЫұЫіЫ№Ы°) |
|
|
#3 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
ШұЩҲШҙ Ш§ШЁШӘЪ©Ш§ШұЫҢ ШіШ§Ш®ШӘ ЩҲ ШЁЩҮШЁЩҲШҜ ШӘЩҲШұ Щ…ШіШҰЩ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮ ЪҜШұШҜ ЩҶШ§Щ…ШӘЩӮШ§ШұЩҶ

|
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | *sepid* (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), arameshn (ЫұЫІ-Ы№-ЫұЫіЫёЫ№), mav (Ы°Ыө-Ыұ-ЫұЫіЫ№ЫІ), mitrashooshtari (Ы°ЫІ-ЫІЫ¶-ЫұЫіЫ№Ыұ), PATRIOTE SAMURAI (ЫұЫ°-ЫұЫҙ-ЫұЫіЫ№Ы°), saeedeh23 (Ы°Ыі-Ыі-ЫұЫіЫ№Ыұ), snowy_ night (ЫұЫІ-ЫІЫө-ЫұЫіЫёЫё), Solsal (Ы°Ыө-Ыұ-ЫұЫіЫ№Ы°), susaaan (Ы°Ыё-ЫІЫ№-ЫұЫіЫ№Ы°) |
|
|
#4 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
Ъ©ШҜ ШӯЩ„ Щ…ШіШ§Щ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮ ЪҜШұШҜ ШЁШ§ Ш§Щ„ЪҜЩҲШұЩҠШӘЩ… ЪҳЩҶШӘЩҠЪ©
|
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | *sepid* (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), alirezakia (Ы°Ыҙ-ЫұЫ№-ЫұЫіЫ№Ы°), arameshn (ЫұЫІ-Ы№-ЫұЫіЫёЫ№), firethumbs (ЫұЫ°-Ыі-ЫұЫіЫ№ЫІ), free bird (Ы°Ыі-ЫұЫІ-ЫұЫіЫ№Ы°), green_Dream (ЫұЫІ-ЫұЫё-ЫұЫіЫёЫё), hosna83 (Ы°Ыё-ЫұЫё-ЫұЫіЫёЫ№), mav (Ы°Ыө-Ыұ-ЫұЫіЫ№ЫІ), mitrashooshtari (Ы°ЫІ-ЫІЫ¶-ЫұЫіЫ№Ыұ), mnarx (Ы°Ы№-Ы·-ЫұЫіЫёЫ№), pampam (ЫұЫ°-Ыі-ЫұЫіЫёЫё), saeedeh23 (Ы°Ыі-Ыі-ЫұЫіЫ№Ыұ), samane_89 (Ы°Ыҙ-Ы№-ЫұЫіЫ№Ы°), shahriar0111 (ЫұЫІ-ЫұЫ¶-ЫұЫіЫ№Ыҙ), snowy_ night (ЫұЫІ-ЫІЫө-ЫұЫіЫёЫё), Solsal (Ы°Ыө-Ыұ-ЫұЫіЫ№Ы°), susaaan (Ы°Ыё-ЫІЫ№-ЫұЫіЫ№Ы°) |
|
|
#5 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
|
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | *sepid* (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), alirezakia (Ы°Ыҙ-ЫұЫ№-ЫұЫіЫ№Ы°), ali_85 (Ы°Ыі-ЫІЫ·-ЫұЫіЫ№Ыұ), firethumbs (ЫұЫ°-Ыі-ЫұЫіЫ№ЫІ), mitrashooshtari (Ы°ЫІ-ЫІЫ¶-ЫұЫіЫ№Ыұ), saeedeh23 (Ы°Ыі-Ыі-ЫұЫіЫ№Ыұ), shahriar0111 (ЫұЫІ-ЫұЫ¶-ЫұЫіЫ№Ыҙ), snowy_ night (ЫұЫІ-ЫІЫө-ЫұЫіЫёЫё), Solsal (Ы°Ыө-Ыұ-ЫұЫіЫ№Ы°), susaaan (Ы°Ыё-ЫІЫ№-ЫұЫіЫ№Ы°) |
|
|
#6 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
 ЩҲ Ш§ЩҠЩҶ ЩҮЩ… ШӘЩҲШ¶ЩҠШӯШ§ШӘ Ъ©Ш§Щ…Щ„ ЩҲ ШЁШұЩҶШ§Щ…ЩҮ ЩҮЩ…ШұШ§ЩҮ ШіЩҲШұШі ШіЩҠ ЩҫЩ„Ш§Ші ЩҫЩ„Ш§Ші |
|
|

|
| Ш§ШІ Astaraki ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | *sepid* (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), alirezakia (Ы°Ыҙ-ЫұЫ№-ЫұЫіЫ№Ы°), arezoooo (Ы°Ыҙ-ЫұЫұ-ЫұЫіЫ№Ыұ), elit (Ы°Ы¶-Ы·-ЫұЫіЫ№Ыұ), firethumbs (ЫұЫ°-Ыі-ЫұЫіЫ№ЫІ), free bird (Ы°Ыі-ЫұЫІ-ЫұЫіЫ№Ы°), hafez11 (Ы°Ы№-ЫұЫі-ЫұЫіЫ№ЫІ), ict69 (Ы°Ы·-ЫІЫө-ЫұЫіЫёЫ№), lesanalgeib (Ы°Ыө-ЫұЫё-ЫұЫіЫ№Ыі), m@r@l (Ы°ЫІ-ЫұЫ°-ЫұЫіЫ№Ыі), minoo007 (Ы°Ыі-ЫұЫ°-ЫұЫіЫ№Ыұ), mitrashooshtari (Ы°ЫІ-ЫІЫ¶-ЫұЫіЫ№Ыұ), sabora (ЫұЫұ-Ы·-ЫұЫіЫ№Ыұ), saeedeh23 (Ы°Ыі-Ыі-ЫұЫіЫ№Ыұ), seda (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), snowy_ night (ЫұЫІ-ЫІЫө-ЫұЫіЫёЫё), Solsal (Ы°Ыө-Ыұ-ЫұЫіЫ№Ы°), susaaan (Ы°Ыё-ЫІЫ№-ЫұЫіЫ№Ы°) |
|
|
#7 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Ш№Ш¶ЩҲ Ш¬ШҜЫҢШҜ
 ШӘШ§ШұЩҠШ® Ш№Ш¶ЩҲЩҠШӘ: ШҜЩҠ ЫұЫіЫёЫё
ЩҫШіШӘ ЩҮШ§: 1
ШӘШҙЩғШұЩҮШ§: 4
5 ШӘШҙЩғШұ ШҜШұ 1 ЩҫШіШӘ
My Mood:

|
|
|
|

|
| Ш§ШІ h.jaza ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ЩҶШҜ: | *sepid* (Ы°Ыө-ЫұЫі-ЫұЫіЫ№Ыұ), mardin200 (ЫұЫ°-ЫІЫө-ЫұЫіЫёЫё), mohammadmono (Ы°Ыұ-ЫІЫ№-ЫұЫіЫ№Ы°), snowy_ night (ЫұЫІ-ЫІЫө-ЫұЫіЫёЫё), Solsal (Ы°Ыө-Ыұ-ЫұЫіЫ№Ы°) |
|
|
#8 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Ш№Ш¶ЩҲ Ш¬ШҜЫҢШҜ
 ШӘШ§ШұЩҠШ® Ш№Ш¶ЩҲЩҠШӘ: Ш§ШіЩҒЩҶШҜ ЫұЫіЫёЫё
ЩҫШіШӘ ЩҮШ§: 3
ШӘШҙЩғШұЩҮШ§: 0
1 ШӘШҙЩғШұ ШҜШұ 1 ЩҫШіШӘ
|
ШЁШ§ ШіЩ„Ш§Щ… Ш®ШҜЩ…ШӘ ШҙЩ…Ш§ ШҜЩҲШіШӘ Ш№ШІЫҢШІ ЩҲШӘШҙЪ©Шұ Ш§ШІ ЩҫШіШӘ Щ…ЩҒЫҢШҜШӘЩҲЩҶ
Ш§ЪҜШұ Ш§Щ…Ъ©Ш§ЩҶ ШҜШ§ШұШҜ ШҜШұ Щ…ЩҲШұШҜ ШӘШ§ШЁШ№ Ш§ШЁШӘЪ©Ш§ШұЫҢ ШЁШұШ§ЫҢ ШӯЩ„ Ш§ЫҢЩҶ Щ…ШіШ§Щ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЪҜШұШҜ ШӘЩҲШ¶ЫҢШӯ ШҜЩҮЫҢШҜ Щ…ЩҶШёЩҲШұЩ… Ш§ЫҢЩҶЩҮ Ъ©ЩҮ ШӘШ§ШЁШ№ Ш§ШЁШӘЪ©Ш§ШұЫҢ Ш§ЫҢЩҶ Щ…ШіШ§Щ„ЩҮ ЪҶЫҢЩҮ (ШҜШұ ШұЩҲШҙ ЪҳЩҶШӘЫҢЪ©) |
|
|

|
|
|
#9 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Ш№Ш¶ЩҲ Ш¬ШҜЫҢШҜ
 ШӘШ§ШұЩҠШ® Ш№Ш¶ЩҲЩҠШӘ: Ш§ШіЩҒЩҶШҜ ЫұЫіЫёЫё
ЩҫШіШӘ ЩҮШ§: 3
ШӘШҙЩғШұЩҮШ§: 1
0 ШӘШҙЩғШұ ШҜШұ 0 ЩҫШіШӘ
|
ШЁШ§ ШіЩ„Ш§Щ…
ШӯЩ„ Щ…ШіШҰЩ„ЩҮ ШӘЫҢ Ш§Ші ЩҫЫҢ ШұЩҲ ШЁШ§ ШІШЁШ§ЩҶ ШіЫҢ ++ ЩҲ ШЁЩҮ ШұЩҲШҙ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ЪҳЩҶШӘЫҢЪ© Щ…ЫҢ Ш®ЩҲШ§ШіШӘЩ… ШЁШ§ ШӘШҙЪ©Шұ 
|
|
|

|
|
|
#10 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Ш№Ш¶ЩҲ Ш¬ШҜЫҢШҜ
 ШӘШ§ШұЩҠШ® Ш№Ш¶ЩҲЩҠШӘ: ШЁЩҮЩ…ЩҶ ЫұЫіЫёЫё
ЩҫШіШӘ ЩҮШ§: 6
ШӘШҙЩғШұЩҮШ§: 0
4 ШӘШҙЩғШұ ШҜШұ 4 ЩҫШіШӘ
|
ШіЩ„Ш§Щ…
Ш§ЪҜШұ Ш§Щ…Ъ©Ш§ЩҶ ШҜШ§ШұШҜ Щ…ЩҶ ШұШ§ ШҜШұ Щ…ЩҲШұШҜ ЩҫЫҢШ§ШҜЩҮ ШіШ§ШІЫҢ Щ…ШіШҰЩ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮ ЪҜШұШҜ ШЁЩҮ Ъ©Щ…Ъ© Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… RBFS ШұШ§ЩҮЩҶЩ…Ш§ЫҢЫҢ Ъ©ЩҶЫҢШҜ ЩҲ ЫҢШ§ ШҜШұ ШөЩҲШұШӘ Ш§Щ…Ъ©Ш§ЩҶ Ш§ЪҜЩҮ Ъ©ШҜЫҢ ШҜШұ Ш§ЫҢЩҶ Щ…ЩҲШұШҜ ШЁЩҮ ЩҮШұ ШІШЁШ§ЩҶЫҢ ШҜШ§ШҙШӘЫҢШҜ ШЁШұШ§ЫҢ Щ…ЩҶ ШҜШұ Ш§ЫҢЩҶ ЩӮШіЩ…ШӘ ШЁЪҜШ°Ш§ШұЫҢШҜ ЩҲ ШҜШұ Щ…ЩҲШұШҜ ШұЩҲШҙЩҮШ§ЫҢ gentic algoritm ЩҲ simulated annearling Ш§ЪҜЩҮ Щ…ЫҢШҙЩҮ Ъ©ШҜ ЩҲ ШұШ§ЩҮ ШӯЩ„ЫҢ ШЁШІШ§ШұЫҢШҜ ШЁШұШ§ЫҢ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮ ЪҜШұШҜ |
|
|

|
| Ш§ШІ amir-shakh ШӘШҙЩғШұ ЩғШұШҜЩҮ Ш§ШіШӘ: | Marzie1998 (Ы°Ыұ-ЫІЫ·-ЫұЫіЫ№Ы№) |
 |
|
«
ШҜШ§ЩҶЩ„ЩҲШҜ ЩҒЫҢЩ„Щ… ШўЩ…ЩҲШІШҙЫҢ ШұЩҲШҙ ЩҮШ§ЫҢ Ъ©ШҜЫҢЩҶЪҜ ЩҫШ§ШіШ® ШҜШұ Щ…ШіШЈЩ„ЩҮ ЩҒШұЩҲШҙЩҶШҜЩҮ ШҜЩҲШұЩҮ ЪҜШұШҜ (ШЁЩҮ ШІШЁШ§ЩҶ ЩҒШ§ШұШіЫҢ
|
NЩҲШІЫҢШұ ШЁШ§ ШұЩҲШҙ local beam search
»
| ЩғШ§ШұШЁШұШ§ЩҶ ШҜШұ ШӯШ§Щ„ ШҜЩҠШҜЩҶ ШӘШ§ЩҫЩҠЪ©: 1 (0 Ш№Ш¶ЩҲ ЩҲ 1 Щ…ЩҮЩ…Ш§ЩҶ) | |
|
|
ШІЩ…Ш§ЩҶ Щ…ШӯЩ„ЩҠ ШҙЩ…Ш§ ШЁШ§ ШӘЩҶШёЩҠЩ… GMT +3.5 ЩҮЩ… Ш§Ъ©ЩҶЩҲЩҶ Ы°Ыі:ЫіЫі ШЁШ№ШҜ Ш§ШІ ШёЩҮШұ Щ…ЩҠШЁШ§ШҙШҜ.








 Hybrid Mode
Hybrid Mode






