 |
Ш§ЩҶШ¬Щ…ЩҶ ШұШ§ ШҜШұ ЪҜЩҲЪҜЩ„ Щ…ШӯШЁЩҲШЁ Ъ©ЩҶЩҠШҜ :
|
|||||||
| Ш«ШЁШӘ ЩҶШ§Щ… | Ш§ШұШіШ§Щ„ ШҜШ№ЩҲШӘЩҶШ§Щ…ЩҮ ШЁЩҮ ШҜЩҲШіШӘШ§ЩҶ ! | ШұШ§ЩҮЩҶЩ…Ш§ЩҠ ШіШ§ЩҠШӘ | Community | ШӘЩӮЩҲЩҠЩ… | Ш§ШұШіШ§Щ„ЩҮШ§ЩҠ Ш§Щ…ШұЩҲШІ | Ш¬ШіШӘШ¬ЩҲ |
 |
| ШӘШЁЩ„ЩҠШәШ§ШӘ ШіШ§ЩҠШӘ | |||||||||||||||||||||||||||||
  |
|
|
LinkBack | Ш§ШЁШІШ§ШұЩҮШ§ЩҠ ШӘШ§ЩҫЩҠЪ© | ЩҶШӯЩҲЩҮ ЩҶЩ…Ш§ЩҠШҙ |
|
|
#1 (Щ„ЫҢЩҶЪ© ШҜШ§ШҰЩ…) |
|
Administrator
 |
ШЁШ®Шҙ ШұЩӮШ§ШЁШӘ Ш§ШіШӘШ№Щ…Ш§ШұЫҢ ШҜШұ ICA ЪҶЪҜЩҲЩҶЩҮ Щ…ШҜЩ„ Щ…ЫҢ ШҙЩҲШҜШҹ
ШіЩҲШ§Щ„: "ШЁШ§ ШҜШұЩҲШҜ ЩҒШұШ§ЩҲШ§ЩҶШҢШЁШ§ШЁШӘ ШӘЩ…Ш§Щ…ЫҢ Ш§Ш·Щ„Ш§Ш№Ш§ШӘЫҢ Ъ©ЩҮ ШҜШұ Щ…ЩҲШұШҜ ICA ШЁШұ ШұЩҲЫҢ ШіШ§ЫҢШӘ(Щ…ШӯШ§ШіШЁШ§ШӘ ШӘЪ©Ш§Щ…Щ„ЫҢ) ЪҜШ°Ш§ШҙШӘЩҮ Ш§ЫҢШҜШҢ Щ…ШӘШҙЪ©ШұЩ…. Щ…ЩҶ Щ…ЫҢвҖҢШ®ЩҲШ§Щ… Ш§ЫҢЩҶ ШӘШұЩ… ICA ШұШ§ ШҜШұ ЩҲШ§ШӯШҜ ШіЩ…ЫҢЩҶШ§ШұЩ… Ш§ШұШ§ШҰЩҮ Ъ©ЩҶЩ…. ШӘЩ…Ш§Щ…ЫҢ Щ…ЩҲШ§ШұШҜ ШұШ§ ШӘЩӮШұЫҢШЁШ§ЩӢ Щ…ШӘЩҲШ¬ЩҮ ШҙШҜЩ…. ЩҲЩ„ЫҢвҖҢ ШҜШұ ЩӮШіЩ…ШӘ "ШұЩӮШ§ШЁШӘ Ш§ШіШӘШ№Щ…Ш§ШұЫҢ" Ш§ШҙЪ©Ш§Щ„ ШҜШ§ШұЩ…. Ш§ЫҢЩҶЪ©ЩҮ ШЁШұШҜШ§Шұ P ШӘШ№ШұЫҢЩҒ Щ…ЫҢвҖҢШҙЩҮ ЩҲ ШЁШ№ШҜ ШЁШұШҜШ§Шұ (ШұЩҶШҜЩ…) R ШӘШ№ШұЫҢЩҒ Щ…ЫҢвҖҢШҙЩҮ ЩҲ ШҜШұ ЩҶЩҮШ§ЫҢШӘ ШҜШ§ШұЫҢЩ…: D = P - R Ш§ЫҢЩҶШ¬Ш§ЩҮШ§ШұЩҲ Щ…ШӘЩҲШ¬ЩҮ ЩҶЩ…ЫҢШҙЩ…. ШҜШұ ШөЩҲШұШӘ Ш§Щ…Ъ©Ш§ЩҶ Щ„Ш·ЩҒШ§ЩӢ ШЁЩҶШҜЩҮ ШұШ§ ШҜШұ Ш§ЫҢЩҶ Щ…ЩҲШұШҜ ШұШ§ЩҮЩҶЩ…Ш§ЫҢЫҢ Ъ©ЩҶЫҢШҜ."  ЩҫШ§ШіШ® Ш§ЫҢЩҶ ШіЩҲШ§Щ„ ШҜШұ Ш§ШҜШ§Щ…ЩҮ ШўЩ…ШҜЩҮ Ш§ШіШӘ. ЩҒШұШ¶ Ъ©ЩҶЫҢЩ… Ъ©ЩҮ 4 ЩҶЩҒШұ ШҜШұ ШЁШ§ЩҶЪ©ЫҢ ШіШұЩ…Ш§ЫҢЩҮ ЪҜШ°Ш§ШұЫҢ Ъ©ШұШҜЩҮ Ш§ЩҶШҜ ЩҲ Щ…ЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… Ш¬Ш§ЫҢШІЩҮ ШіЩҒШұ ШЁЩҮ ШҜЩҲШұ ШҜЩҶЫҢШ§ ШұШ§ ШЁЩҮ ЫҢЪ©ЫҢ Ш§ШІ ШўЩҶЩҮШ§ ШЁШҜЩҮЫҢЩ…. ЩҮШұ ШЁШ§ЩҶЪ©ЫҢ ШЁШұШ§ЫҢ Ш®ЩҲШҜ ШіЫҢШ§ШіШӘ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ Ш®Ш§ШөЫҢ ШҜШ§ШұШҜ. Щ…Ш«Щ„Ш§ЩӢ ШЁШ§ЩҶЪ©ЫҢ Щ…ЫҢ ЪҜЩҲЫҢШҜ "ШЁШҙШӘШ§ШЁЫҢШҜ! ЩҮШұ ЩҫЩҶШ¬Ш§ЩҮ ЩҮШІШ§Шұ ШұЫҢШ§Щ„ ШҜШұ ЩҮШұ ШұЩҲШІ ЫҢЪ© Ш§Щ…ШӘЫҢШ§ШІ". ШЁШ§ЩҶЪ© ШҜЫҢЪҜШұ Щ…ЫҢ ЪҜЩҲЫҢШҜШҢ "ЩҮШұ 10 ЩҮШІШ§Шұ ШұЫҢШ§Щ„ ШҜШұ ЩҮШұ Щ…Ш§ЩҮ ЫҢЪ© Ш§Щ…ШӘЫҢШ§ШІ". ЫҢШ§ Ш§ШөЩ„Ш§ЩӢ ШЁШ§ЩҶЪ© ШҜЫҢЪҜШұ Щ…ЫҢ ЪҜЩҲЫҢШҜ: "Щ…ЩҲШ¬ЩҲШҜЫҢ ШӯШіШ§ШЁ Щ…ЩҮЩ… ЩҶЫҢШіШӘ. Щ…ЩҲШ¬ЩҲШҜЫҢ ШЁШ§Щ„Ш§ЫҢ 10 ЩҮШІШ§Шұ ШұЫҢШ§Щ„ ЩҮШұ ЪҶЩӮШҜШұ ШЁШ§ШҙШҜШҢ ЫҢЪ© Ш§Щ…ШӘЫҢШ§ШІ". ЩҮШұ ЫҢЪ© Ш§ШІ ШіЫҢШ§ШіШӘ ЩҮШ§ЫҢ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ ЩҒЩҲЩӮ ШЁЩҮ ЩҶЩҒШ№ ЩӮШҙШұ Ш®Ш§ШөЫҢ ЩҮШіШӘЩҶШҜ. Щ…Ш«Щ„Ш§ЩӢ ШұЩҲШҙ Ш§ЩҲЩ„ ШЁШұШ§ЫҢ Ш§ЩҒШұШ§ШҜ ШЁШ§ ШіШұЩ…Ш§ЫҢЩҮ ШЁШ§Щ„Ш§ ЩҲЩ„ЫҢ ШЁШ§ ШӯШіШ§ШЁ Щ…ШӘШәЫҢШұШҢ ШұЩҲШҙ ШҜЩҲЩ… ШЁШұШ§ЫҢ Ш§ЩҒШұШ§ШҜ ШЁШ§ ШіШұЩ…Ш§ЫҢЩҮ ШЁШ§Щ„Ш§ ЩҲЩ„ЫҢ ШЁШ§ ШӯШіШ§ШЁ ШіЩҫШұШҜЩҮ Ш«Ш§ШЁШӘ ЩҲ ШұЩҲШҙ ШўШ®Шұ ЩҮЩ… ШЁШұШ§ЫҢ Ш§ЩҒШұШ§ШҜ ШўШіЫҢШЁ ЩҫШ°ЫҢШұ ЩҲ ЩӮШҙШұ ЩҫШ§ШЁШұЩҮЩҶЩҮ Ш¬Ш§Щ…Ш№ЩҮ Ш®ЩҲШЁ Ш§ШіШӘ ЩҲ Щ…ЩҶ Ш®ЩҲШҜЩ… ШӘШұШ¬ЫҢШӯ Щ…ЫҢ ШҜЩҮЩ… ШҜШұ ЪҶЩҶЫҢЩҶ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ ШЁШ§ШҙЩ… ЪҶЩҲЩҶ ШЁШ§ ЩҮЩ…ЩҮ ШіШұЩ…Ш§ЫҢЩҮ ШҜШ§ШұЩҮШ§ ЫҢЪ© Ш§Щ…ШӘЫҢШ§ШІ Ш®ЩҲШ§ЩҮЩ… ШҜШ§ШҙШӘ. Ш§ШІ ШЁШӯШ« ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ Ш®Ш§ШұШ¬ ШҙЩҲЫҢЩ…. ШЁШҜЩҲЩҶ ШӘЩҲШ¬ЩҮ ШЁЩҮ Щ…Ш§ЩҮЫҢШӘ ШұЩҲШҙ Ш§Щ…ШӘЫҢШ§ШІ ШҜЩҮЫҢ ЩҒЩҲЩӮШҢ ЩҒШұШ¶ Ъ©ЩҶЫҢЩ… 4 ЩҶЩҒШұ ШЁЩҮ ШӘШұШӘЫҢШЁ Ш§Щ…ШӘЫҢШ§ШІ ЩҮШ§ЫҢ ШІЫҢШұ ШұШ§ Ъ©ШіШЁ Ъ©ШұШҜЩҮ Ш§ЩҶШҜ. ЩғШҜ:
Point = [1 2 3 4]; Щ…ЫҢ ШӘЩҲШ§ЩҶ Ш§ШӯШӘЩ…Ш§Щ„ ШЁШұЩҶШҜЩҮ ШҙШҜЩҶ ШІЫҢШұ ШұШ§ ШЁЩҮ ШўЩҶЩҮШ§ Ш§Ш®ШӘШөШ§Шө ШҜШ§ШҜ. ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ Ш§Щ…ШӘЫҢШ§ШІ ЩҮШ§ЫҢ ЩҒЩҲЩӮ 10 Ш§ШіШӘ. ЩҫШі Ш§Щ…ШӘЫҢШ§ШІЩҮШ§ ШұШ§ ШӘЩӮШіЫҢЩ… ШЁШұ Щ…Ш¬Щ…ЩҲШ№ Ш§Щ…ШӘЫҢШ§ШІ ЩҮШ§ Щ…ЫҢ Ъ©ЩҶЫҢЩ…. ЩғШҜ:
Probability = [1 2 3 4] / 10 = [0.1 0.2 0.3 0.4]; ШӯШ§Щ„ ЫҢЪ© ШЁШұШҜШ§Шұ ШӘШөШ§ШҜЩҒЫҢ (ШұЩҶШҜЩ…) Ш§ЫҢШ¬Ш§ШҜ Щ…ЫҢ Ъ©ЩҶЫҢЩ…. Ш§ЫҢЩҶ Ъ©Ш§Шұ ШұШ§ ШЁШ§ ШҜЪ©Щ…ЩҮ rnd ШҜШұ Щ…Ш§ШҙЫҢЩҶ ШӯШіШ§ШЁ ЩҲ ЫҢШ§ ШҜШұШіШӘЩҲШұ rand ШҜШұ Щ…ШӘЩ„ШЁ Ш§ЩҶШ¬Ш§Щ… Щ…ЫҢ ШҜЩҮЫҢЩ…. Щ…ЩҶ ШЁШ§ ШӘЩҲЩ„ЫҢШҜ Ш§ЫҢЩҶ ШЁШұШҜШ§Шұ ШӘШөШ§ШҜЩҒЫҢ ШҜШұ Щ…ШӘЩ„ШЁ ШЁЩҮ ЩҶШӘЫҢШ¬ЩҮ ШІЫҢШұ ШұШіЫҢШҜЩ… (Щ…Ш·Щ…ШҰЩҶ ШЁШ§ШҙЫҢШҜ ШӘЩӮЩ„ШЁЫҢ ШҜШұ Ъ©Ш§Шұ ЩҶЫҢШіШӘ!). ЩғШҜ:
R = 0.82 0.96 0.13 0.91]; ШӯШ§Щ„ ШЁЫҢШ§ЫҢШҜ R ШұШ§ Ш§ШІ P Ъ©Щ… Ъ©ЩҶЫҢЩ… ЩҲ Ш§ЩҶШҜЫҢШі Щ…Ш§Ъ©ШІЫҢЩ…Щ… ШұШ§ ЩҫЫҢШҜШ§ Ъ©ЩҶЫҢЩ…. ЩғШҜ:
Probability - R = [0.1 0.2 0.3 0.4] - [0.82 0.96 0.13 0.91] = [ -0.71 -0.71 0.17 -0.51]; ШЁЫҢШҙШӘШұЫҢЩҶ Ш№ШҜШҜ ШҜШұ ШЁШұШҜШ§Шұ ШЁШ§Щ„Ш§ ШЁШұШ§ШЁШұ 0.17 ЩҲ Щ…ШұШЁЩҲШ· ШЁЩҮ ШіШұЩ…Ш§ЫҢЩҮ ЪҜШ°Ш§Шұ ШіЩҲЩ… Ш§ШіШӘ. ШӘЪ©ШұШ§Шұ ШЁШ§ШұЩҮШ§ЫҢ Щ…Ш®ШӘЩ„ЩҒ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ ШЁШ§ ЩҮЩ…Ш§ЩҶ Ш§ШӯШӘЩ…Ш§Щ„Ш§ШӘ ШЁШұЩҶШҜЩҮ ШҙШҜЩҶ ШЁШ§Щ„Ш§ШҢ ЩҶШӘЫҢШ¬ЩҮ ШЁШұЩҶШҜЩҮ Щ…ШӘЩҒШ§ЩҲШӘЫҢ Ш®ЩҲШ§ЩҮШҜ ШҜШ§ШҙШӘ. Ш§Щ…Ш§ ШЁШЁЫҢЩҶЫҢЩ… Ш§ЪҜШұ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ 10000 ШЁШ§Шұ ШӘЪ©ШұШ§Шұ ШҙЩҲШҜШҢ ЩҮШұ ШіШұЩ…Ш§ЫҢЩҮ ЪҜШ°Ш§Шұ ШЁЩҮ ШӘШұШӘЫҢШЁ ЪҶЩҶШҜ ШЁШ§Шұ ШЁШұЩҶШҜЩҮ Щ…ЫҢ ШҙЩҲШҜШҹ ЫҢШ№ЩҶЫҢ ШўЫҢШ§ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ Щ…ЩҶШөЩҒШ§ЩҶЩҮ (Fair) Ш§ШіШӘШҹ Ш§ЫҢЩҶЪҜЩҲЩҶЩҮ ЩҶШЁШ§ШҙШҜ Ъ©ЩҮ ЩҒШұШҜЫҢ ШЁШ§ ШіШұЩ…Ш§ЫҢЩҮ ЪҜШ°Ш§ШұЫҢ ШЁЫҢШҙШӘШұШҢ ШҜШұ ШӘШ№ШҜШ§ШҜ Ъ©Щ…ШӘШұЫҢ ШЁШұЩҶШҜЩҮ ШҙЩҲШҜШҹ!! ШЁШұШ§ЫҢ ШӘШіШӘ ШұЩҲШҙ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ ШЁШұЩҶШ§Щ…ЩҮ ШІЫҢШұ ШұШ§ ШҜШұ Щ…ШӘЩ„ШЁ ЩҶЩҲШҙШӘЫҢЩ…. ЩғШҜ:
IndexeMat = zeros(1,4);
P = [.1 .2 .3 .4];
for ii = 1:10000
R = rand(1,4);
D = P - R;
Index = find(D == max(D));
IndexeMat(Index) = IndexeMat(Index) + 1;
end
IndexeMat = IndexeMat
ЩҶШӘЫҢШ¬ЩҮ ЫҢЪ© ШЁШ§Шұ Ш§Ш¬ШұШ§ЫҢ ШЁШұЩҶШ§Щ…ЩҮ (ШӘШ№ШҜШ§ШҜ ШЁШұЩҶШҜЩҮ ШҙШҜЩҶ) ШҜШұ ШІЫҢШұ ШўЩ…ШҜЩҮ Ш§ШіШӘ. ЩғШҜ:
IndexeMat = [986 1743 2853 4418] ЩҮЩ…Ш§ЩҶШ·ЩҲШұ Ъ©ЩҮ Щ…ЫҢ ШЁЫҢЩҶЫҢШҜШҢ Ш§ЩҒШұШ§ШҜ ШЁЩҮ ШӘШұШӘЫҢШЁ ШЁШіШӘЩҮ ШЁЩҮ Ш§Щ…ШӘЫҢШ§ШІШҙШ§ЩҶ (Ш§ШӯШӘЩ…Ш§Щ„ШҙШ§ЩҶ)ШҢ ШӘШ№ШҜШ§ШҜЫҢ Ш§ШІ Ш§ЫҢЩҶ 10000 ШЁШ§Шұ ШұШ§ ШЁШұШҜЩҮ Ш§ЩҶШҜ. ШҙЩ…Ш§ ЩҮЩ… ШЁШ§ Ш§Ш¬ШұШ§ЫҢ Ш§ЫҢЩҶ ШЁШұЩҶШ§Щ…ЩҮ ШЁШ§ЫҢШҜШҢ ЩҶШӘШ§ЫҢШ¬ ШӘЩӮШұЫҢШЁШ§ЩӢ Щ…ШҙШ§ШЁЩҮЫҢ ШЁЪҜЫҢШұЫҢШҜ. 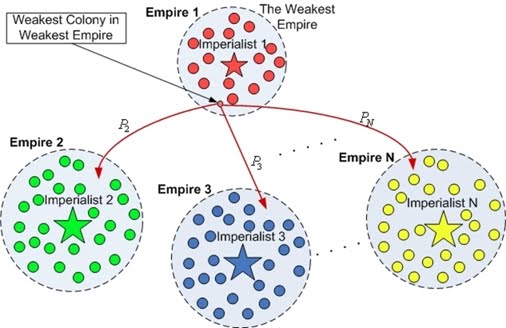 ШұЩҲЩҶШҜ ЩҒЩҲЩӮ ШҜЩӮЫҢЩӮШ§ЩӢ ЩҮЩ…Ш§ЩҶ ШұЩҲЩҶШҜЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШЁШ®Шҙ "ШұЩӮШ§ШЁШӘ Ш§ШіШӘШ№Щ…Ш§ШұЫҢ" ЫҢШ§ (Imperialistic Competition) ШҜШұ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ШұЩӮШ§ШЁШӘ Ш§ШіШӘШ№Щ…Ш§ШұЫҢ Ш§ЩҶШ¬Ш§Щ… Щ…ЫҢ ШҙЩҲШҜ. ШҜШұ Ш§ЫҢЩҶ ШЁШ®Шҙ Щ…ШіШӘШ№Щ…ШұЩҮ Ш¶Ш№ЫҢЩҒ ШЁЩҮ Щ…Ш§ЩҶЩҶШҜ Ш¬Ш§ЫҢШІЩҮ ЩҲ ЩҮШұ Ш§ШіШӘШ№Щ…Ш§ШұЪҜШұ ШЁЩҮ Щ…Ш§ЩҶЩҶШҜ ШіШұЩ…Ш§ЫҢЩҮ ЪҜШ°Ш§Шұ ШҜШұ Щ…ШіШҰЩ„ЩҮ ШЁШ§Щ„Ш§ Ш№Щ…Щ„ Щ…ЫҢ Ъ©ЩҶШҜ. ШҜШұ ЩҶЩҮШ§ЫҢШӘ ЩҮШұ Ш§Щ…ЩҫШұШ§Ш·ЩҲШұЫҢ ШЁШіШӘЩҮ ШЁЩҮ ЩӮШҜШұШӘ (Щ…Ш№Ъ©ЩҲШі ЩҮШІЫҢЩҶЩҮ Ш®ЩҲШҜ) Ш§ШӯШӘЩ…Ш§Щ„ЫҢ ШЁШұШ§ЫҢ Ш§ЩҶШӘШ®Ш§ШЁ Ш§ЫҢЩҶ Ш¬Ш§ЫҢШІЩҮ ШҜШ§ШұШҜ ЩҲ Щ…Ш·Ш§ШЁЩӮ ШұЩҲЩҶШҜ ШЁШ§Щ„Ш§ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ ШЁШұШ§ЫҢ ШӘЩӮШҜЫҢЩ… Ш§ЫҢЩҶ Ш¬Ш§ЫҢШІЩҮ Ш§ЩҶШ¬Ш§Щ… Щ…ЫҢ ШҙЩҲШҜ ЩҲ Ъ©ШҙЩҲШұ ШЁШ§ ЩӮШҜШұШӘ ШЁЫҢШҙШӘШұ ЩҶЩҮ ЩҮЩ…ЫҢШҙЩҮ ЩҲЩ„ЫҢ ШҜШұ ШЁШ§ШұЩҮШ§ЫҢ ШЁЫҢШҙШӘШұЫҢ ШЁШұЩҶШҜЩҮ Ш§ЫҢЩҶ ЩӮШұШ№ЩҮ Ъ©ШҙЫҢ (ЩҲ ШҙШ§ЫҢШҜ ЩҶШІШ§Ш№ Ш®ЩҲЩҶЫҢЩҶ) Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. Ш§ЫҢЩҶ ШұЩҲШҙ ШұШ§ ШЁШ§ ЪҶШұШ®ЩҮ ШұЩҲЩ„ШӘ (Roulette Wheel) ШҜШұ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ЪҳЩҶШӘЫҢЪ© (Genetic Algorithms) Щ…ЩӮШ§ЫҢШіЩҮ Ъ©ЩҶЫҢШҜ. ШЁЩҮ ЩҶШёШұ ШҙЩ…Ш§ ЩҶЩӮШ·ЩҮ Ш¶Ш№ЩҒ ЩҲ ШЁШұШӘШұЫҢ ЩҮШұ ШұЩҲШҙ ЪҶЫҢШіШӘШҹ ШҙЩ…Ш§ Ъ©ШҜШ§Щ… ШұЩҲШҙ ШұШ§ ШЁШұШ§ЫҢ Ш§ШіШӘЩҒШ§ШҜЩҮ ШҜШұ ЫҢЪ© Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ШӘЪ©Ш§Щ…Щ„ЫҢ Щ…ЩҶШ§ШіШЁ ШӘШұ Щ…ЫҢ ШҜШ§ЩҶЫҢШҜШҹ  Щ…ЩҶШЁШ№ : ШЁШ®Шҙ ШұЩӮШ§ШЁШӘ Ш§ШіШӘШ№Щ…Ш§ШұЫҢ ШҜШұ ica ЪҶЪҜЩҲЩҶЩҮ Щ…ШҜЩ„ Щ…ЫҢ ШҙЩҲШҜШҹ
__________________
       ЩҲЩҠШұШ§ЩҠШҙ ШҙШҜЩҮ ШӘЩҲШіШ· Astaraki; ЫұЫ°-Ы·-ЫұЫіЫёЫ№ ШҜШұ ШіШ§Ш№ШӘ Ы°Ыұ:ЫіЫё ШЁШ№ШҜ Ш§ШІ ШёЩҮШұ |
|
|

|
| #ADS | |
|
ЩҶШҙШ§ЩҶ ШҜЩҮЩҶШҜЩҮ ШӘШЁЩ„ЫҢШәШ§ШӘ
ШӘШЁЩ„ЩҠШәЪҜШұ
ШӘШ§ШұЩҠШ® Ш№Ш¶ЩҲЩҠШӘ: -
Щ…ШӯЩ„ ШіЩғЩҲЩҶШӘ: -
ШіЩҶ: 2010
ЩҫШіШӘ ЩҮШ§: -
|
|
|
|
 |
«
Ш§ШіЩ„Ш§ЩҠШҜЩҮШ§ЩҠ ШўЩ…ЩҲШІШҙЩҠ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ШұЩӮШ§ШЁШӘ Ш§ШіШӘШ№Щ…Ш§ШұЫҢ
|
ЩҒЫҢЩ„Щ…: Ъ©Ш§ШұШЁШұШҜ Ш§Щ„ЪҜЩҲШұЫҢШӘЩ… ШұЩӮШ§ШЁШӘ Ш§ШіШӘШ№Щ…Ш§ШұЫҢ ШҜШұ ШӯЩ„ Щ…Ш№Ъ©ЩҲШі ШҙШЁЪ©ЩҮ Ш№ШөШЁЫҢ
»
| ЩғШ§ШұШЁШұШ§ЩҶ ШҜШұ ШӯШ§Щ„ ШҜЩҠШҜЩҶ ШӘШ§ЩҫЩҠЪ©: 1 (0 Ш№Ш¶ЩҲ ЩҲ 1 Щ…ЩҮЩ…Ш§ЩҶ) | |
|
|
ШІЩ…Ш§ЩҶ Щ…ШӯЩ„ЩҠ ШҙЩ…Ш§ ШЁШ§ ШӘЩҶШёЩҠЩ… GMT +3.5 ЩҮЩ… Ш§Ъ©ЩҶЩҲЩҶ Ы°Ыҙ:ЫіЫ· ЩӮШЁЩ„ Ш§ШІ ШёЩҮШұ Щ…ЩҠШЁШ§ШҙШҜ.





 Linear Mode
Linear Mode







