در
مقدمه ای به هوش مصنوعی سه بخش اساسی در
هوش مصنوعی رو بطور خیلی خلاصه گفتیم! حالا توی این بخش می خوایم بطور خلاصه به شبکه های عصبی بپردازیم.

ببخشید؟

" آخه من که هنوز چیزی نگفتم که می خوای سوال کنی! سوالت چیه حالا؟ "

من یادم رفت اون سه بخش اساسی چی بودن. می شه یک بار دیگه بگید؟

" سه بخش عبارتند از:
- شبکه های عصبی یا Neural Network
- الگوریتم ژنتیک یا Genetic Algorithm
- منطق فازی یا Fuzzy Logic
البته به این راحتی نمیشه
هوش مصنوعی رو دسته بندی کرد. منظورمون از این دسته بندی این هست که این روز ها روی این ۳ مبحث بیشتر بحث می شه. "
خوب کسی یادش هست شبکه های عصبی هدف و خاصیت هاش چی بود؟

من تا جایی که یادمه در
شبکه های عصبی مصنوعی یا Artificial Neural Networks محققان قصد داشتند که طریقه ی عملکرد مغز انسان در به خاطر سپردن اطلاعات و یادگیری رو شبیه سازی کنند.
محققان توی تحقیق هاشون دیدن که مغز انسان از تعداد خیلی زیادی عصب یا Neuron تشکیل شده که هر کدوم از این عصب ها به تعداد دیگه ای عصب متصل هستن و به همدیگه سیگنال هایی رو میفرستند. در بعضی شرایط عصب ها سیگنال رو از خودشون عبور میدن و اون رو تقویت می کنند و در بعضی شرایط هم از خودشون عبور نمیدن. با اینکه هر نورون ساختار خیلی پیچیده ای نداره مجموعه ی این نورون ها یک شبکه ی بسیار پیچیدرو تشکیل میده که قابلیت یادگیری و ذخیره کردن اطلاعات و تحلیل اون ها رو داره!

" بسیار عالی! خیلی خوشحالم که خوب حرف های جلسه ی قبل یادت مونده! همونطوری که دوستمون گفتن مغز انسان تعداد خیلی زیادی نورون داره که حدودا ۱۰ به توان ۱۲ تا می شه. ولی هر نورون حدودا فقط به ۱۰ به توان ۳ نورون دیگه وصل هست که این نشون می ده ارتباطات بین این نورون ها انتخاب شده هست!
خوب حالا کسی یادش هست که محققا به چه نحوی سعی کردند شبکه های عصبی رو شبیه سازی کنند؟ "

تا جایی که من یادم هست گفتید اول نورون های مصنوعی رو تعریف می کنند به این صورت که هر نورون یه تعداد ورودی و خروجی داره و یک بایاس و هر ورودی هم یک وزن (Weight) داره.
بعد این نورون ها رو توی چند لایه قرار می دن که به لایه ی اول لایه ی ورودی و به آخرین لایه لایه ی خروجی و به بقیه ی لایه ها لایه ی مخفی یا میانی میگن. تعداد نورون های لایه ی ورودی و خروجی بسته به تعداد ورودی و خروجی تعیین می شن اما تعداد لایه های میانی و نورون های هر لایه می تونه هر مقداری باشه که البته هر مقداری از اون نتیجه ی مطلوبی رو به ما نمیده و باید انتخاب شده باشه.
عالیه! ممنونم از همکاریتون!
البته نورون ها فقط از بخش هایی که شما گفتید تشکیل نمی شن و ممکن هست بر حسب نوع شبکه پارامتر های دیگری هم داشته باشن که بعدا بهشون اشاره می کنیم.
پرسپترون (Perceptron)
تا اینجا از دور به ساختار نورون ها و
شبکه ی عصبی نگاه کردیم. حالا می خوایم آسون ترین شکل نورون رو در ساده ترین حالت بررسی کنیم.
پرسپترون یا Perceptron ساده ترین نوع مدلسازی نورون هست. از اونجایی که بررسی چند پرسپترون در لایه های مختلف کمی پیچیده هست برای شروع به بررسی یک عدد پرسپترون می پردازیم.
پرسپترون دارای یک سری ورودی خارجی. یک ورودی داخلی به نام
بایاس (bias). یک threshold و یک خروجی هست. که در شکل سمت چپ می تونید اون رو ببینید!

پرسپترون
هر پرسپترون نشاندهنده و معرف یک نورون هست. ورودی پرسپترون ها معمولا از جنس boolean هست اما در کل می تونه هر عددی باشه ولی خروجی
همیشه یک boolean هست!

ببخشید! منظورتون از boolean چی هست دقیقا؟

" مثلا وقتی می گیم خروجی یک پرسپترون همیشه boolean یا بولین هست یعنی خروجی می تونه دو مقدار ۱ و ۰ داشته باشه! که ۱ معرف درست یا true و ۰ معرف غلط یا false هست. "

پس یعنی ورودی پرسپترون می تونه هر مقداری باشه اما معمولا یا ۰ یا ۱ هست و خروجی اون ۱۰۰٪ ۰ یا ۱ هست. درسته؟

" بله! کاملا درسته... "
در صورتی که خروجی یک پرسپترون یک باشه به اون پرسپترون می گیم
پرسپترون فعال یا activated.
تمام ورودی ها از جمله بایاس دارای یک وزن هستند که این وزن ضرب در مقدار ورودی می شه. معمولا وزن بایاس برابر ۱ هست.
یکی از مهمترین عوامل هر نورون
تابع فعال کننده یا Activation function اون نورون هست. تابع فعال کننده تعیین می کنه که با توجه به ورودی های نورون خروجی اون به چه شکل باشه. در پرسپترون ها ما یکی از ساده ترین توابع فعال کنندرو داریم. این تابع تمام ورودی های پرسپترون رو بعد از ضرب کردن اون ها در وزنشون با هم جمع می کنه. در صورتی که جمع اونا از
threshold بیشتر یا مساوی بود خروجی ۱ خواهد بود یعنی پرسپترون فعال خواهد شد و در غیر این صورت پرسپترون غیر فعال خواهد شد. پس در صورتی که شرط زیر برقرار باشه یک پرسپترون فعال خواهیم داشت:
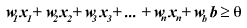
در اصل threshold مثل یک دیوار می مونه. اگر سیگنال انرژی کافی برای رد شدن از دیوار رو داشته باشه از روی اون عبور می کنه. در غیر این صورت پشت دیوار می مونه.
یادگیری در پرسپترون
از خصیصه های اصلی پرسپترون ها قابلیت
یادگیری یا train شدن هست. این یادگیری در پرسپترون ها supervised هست. به این مفهوم که ما باید تعدادی ورودی به همراه خروجی صحیح داشته باشیم تا پرسپترون بتونه اون رو تقلید کنه.
یادگیری پرسپترون ها با این صورت هست:
- یک خروجی تولید می کنند.
- خروجی رو با خروجی که باد می بوده مقایسه می کنند.
- خودشون رو کمی تنظیم می کنند تا به خروجی نزدیک تر بشن.
بعد از تکرار شدن این مراحل به تعداد کافی پرسپترون اصتلاحا به رفتار صحیح همگرا یا converge میشه!
به این روش یادگیری
delta rule یا قانون دلتا می گن. در این روش یادگیری تغییر وزن در هر مرحله به صورت زیر محاسبه می شه:
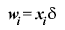
که دلتا در اون تفاوت خروجی مورد نظر و خروجی نورون بوده و xi مقدار ورودی هست.

پس یعنی
مقدار جدید وزن هر نورون می شه تفاوت خروجی مورد نظر و خروجی نورون ضرب در مقدار ورودی اون نورون؟

" به جز قسمت اول بقیه ی حرفت درسته. این مقدار وزن جدید نیست بلکه
به وزن قبلی اضافه میشه! "

پس یعنی مقداری که بدست میاد میزان تغییرات در وزن قبلی هست! الآن متوجه شدم.

" بسیار عالی. "
مثال تابع OR
یک پرسپترون قابلیت جدا کردن فضا به
دو بخش رو داره. پس ما با یک پرسپترون فقط می تونیم توابعی رو به درستی بدست بیاریم که در فضا بتونیم قسمت های مثبت خروجی و منفی اون رو به دو قسمت تقسیم کنیم.
در شکل زیر تونستیم به یک پرسپترون تابع OR رو یاد بدیم.
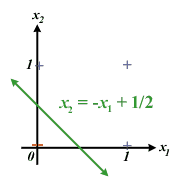
دو محور دو ورودی پرسپترون هستند. همونطور که می بینید پرسپترون فضا رو به دو قسمت مجزا کرده به این صورت که فضای بالای خط سبز رنگ خروجی + یا ۱ خواهند داشت و فضای پایین خط خروجی - یا ۰. پس در صورتی که ورودی ها ۱ و ۱ یا ۰ و ۱ یا ۱ و ۰ باشند خروجی ما + یا ۱ خواهد بود و در صورتی که ورودی ها ۰ و ۰ باشند خروجی - یا - خواهد بود! پس تونستیم با یک پرسپترون ساده تابع OR رو بخوبی در بیاریم.

ببخشید معادله ی این خط رو ما بهش دادیم؟

" نه! اگر معادله ی خط رو ما می دادیم که دیگه یادگیری در کار نبود! ما برای پرسپترون چندین بار مثال زدیم و پروسه ی یادگیری که بالا توضیح دادم به همون تعداد دفعه اجرا شده. یعنی مثلا دو ورودی رو ۱ دادیم و گفتیم خروجی باید ۱ باشه. بعد یک ورودی ۱ و یک ورودی ۰ دادیم و گفتیم خروجی باید ۱ باشه و بعد دو ورودی ۰ دادیم و گفتیم خروجی باید - باشه! و همین کار رو چندین بار تکرار کردیم. و پرسپترون با استفاده از تابع یادگیری فضا رو به دو قسمت مثبت و منفی تقسیم کرده. "

خوب کل حالات OR ۴ حالت بیشتر نمیشن! اینطور که شما میگید ما بیشتر از ۴ مثال برای پرسپترون می زنیم. یعنی ممکنه چندین بار یک مثال رو برای پرسپترون بزنیم؟

" بله! برای اینکه پرسپترون بهتر یاد بگیره ممکن هست مثلا ورودی ۱ و ۱ با جواب ۱ رو چندین بار برای اون مثال بزنیم تا این ورودی ها به همراه خروجی چندین بار داخل تابع یادگیری برن و اطمینان پیدا کنیم پرسپترون همگرا شده! "

من نمی فهمم! خوب این چه کاریه. می تونستیم جای اینکه ۱۰۰ تا مثال بزنیم از اول ۴ تا حالت رو تعریف کنیم! اونطوری نیازی به همگرایی و این جور چیزا هم نبود!

" در مورد این مثال که ۴ حالت بیشتر نیست درست میگید! اما این فقط یک مثال ساده هست برای اینکه مطلب جا بیفته! برای کار های سخت تر مثل شناسایی دست خط تعداد حالات ۴ عدد نیست! نکته ی اصلی این هست که در شبکه های عصبی ما یادگیری داریم! مثلا می تونیم با چند بار نوشتن حرف ب و چند بار نوشتن حرف ج به کامپیوتر یاد بدیم این دو حرف با هم فرق دارند و اولی ب و دومی ج هست! در جلسات بعدی احتمالا همچین مثالی رو نشونتون خواهم داد. "

یک سوال دیگه! پس با یک پرسپترون ما می تونیم تابع AND رو هم در بیاریم! درسته؟

" کاملا درسته! چون تابع AND هم قابل تقسیم به دو بخش در فضا هست. "

XOR چطور؟

" نه! XOR رو نمیشه با یک پرسپترون در آورد! چون XOR با تقسیم فضا به دو بخش مثبت و منفی در نمیاد.
در XOR ورودی و خروجی به این صورته:
- به ازای ۰ و ۰ خروجی ۰ داریم.
- به ازای ۰ و ۱ خروجی ۱ داریم.
- به ازای ۱ و ۰ خروجی ۱ داریم.
- به ازای ۱ و ۱ خروجی ۰ داریم.
یعنی با توجه به شکل آخر بالا سمت راست و پایین سمت چپ خروجی باید + بشه و در بالا سمت چپ و پایین سمت راست باید منفی بشه! ما نمی تونیم هیچ خط راستی رسم کنیم که فضا رو به این صورت تقسیم کنه پس هیچ وقت پرسپترون همگرا نخواهد شد! "
پس فهمیدیم یک پرسپترو محدود هست. اما با ترکیب همین پرسپترون های خیلی محدود در لایه های مختلف می تونیم توابعی مثل XOR و توابع خیلی پیچیده تر از اون رو هم در بیاریم.
انشاالله در جلسات بعدی مثال های بیشتری در ارتباط با شبکه های عصبی خواهیم دید. دیگه خیلی حرف زدم!
موفق باشید.
منبع:
سیاوش محمودیان - بلاگ - مقدمه ای بر شبکه های عصبی